Back in the ___

Table of Contents

1. Lec 6 Solution of linear dynamical systems. System stability.
   1. I. Linear Algebra Recall
      1. a. Definition.
      2. b. Example
      3. c. Definition
      4. d. Example
      5. e. Definition
      6. f. Example
      7. g. Matlab functions
   2. II. Solution of linear dynamical systems
      1. a. Definition
      2. b. Example
      3. c. Definition
      4. d. Lagrange’s formula
      5. e. Example
   3. III. Stability
      1. a. Marginal stability
         1. 1. Neutral Type
         2. 2. Oscillatory Type
      2. b. Asymptotic stability
      3. c. Qualitative behaviour of linear systems
         1. 1. node behaviour
         2. 2. Saddle behaviour
         3. 3. Spiral Behaviour (stable/unstable focus)
         4. 4. Center behaviour
      4. d. Examples

Lec 6 Solution of linear dynamical systems. System stability.

I. Linear Algebra Recall

a. Definition.

b. Example

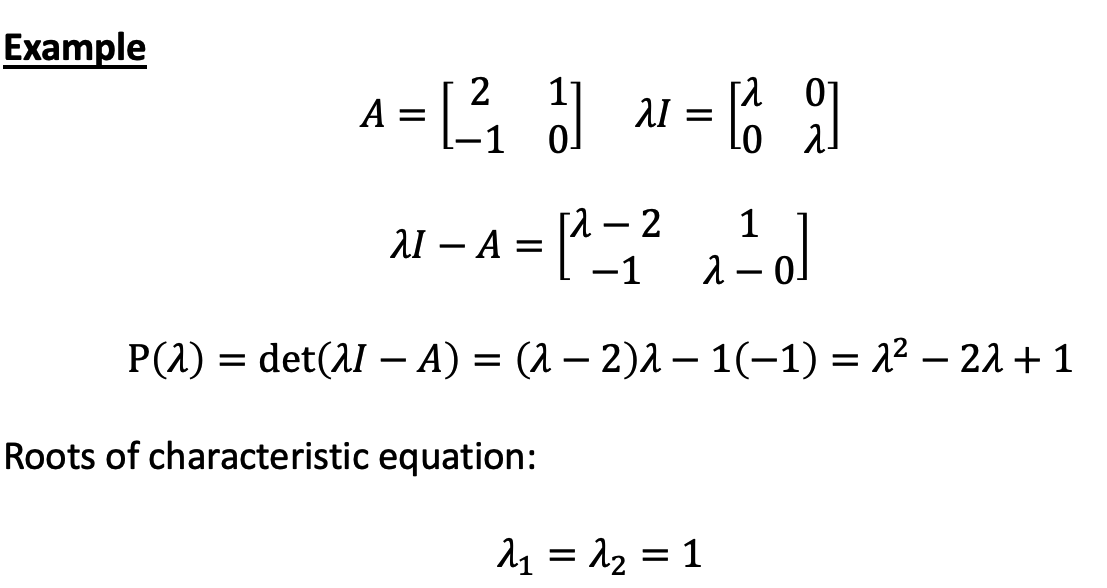
c. Definition

d. Example

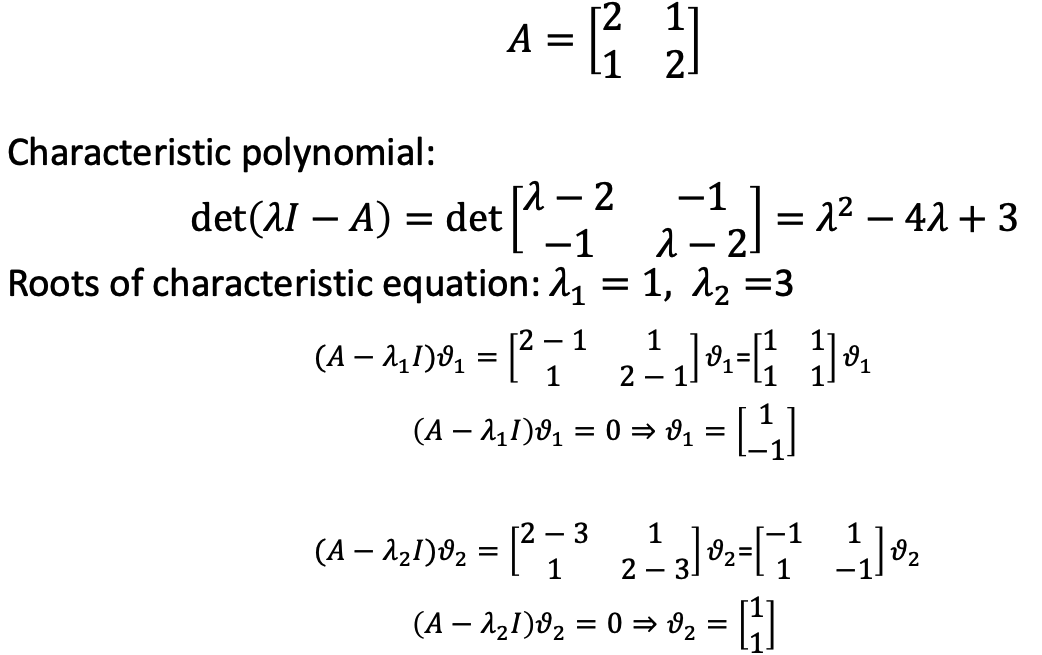
e. Definition

f. Example

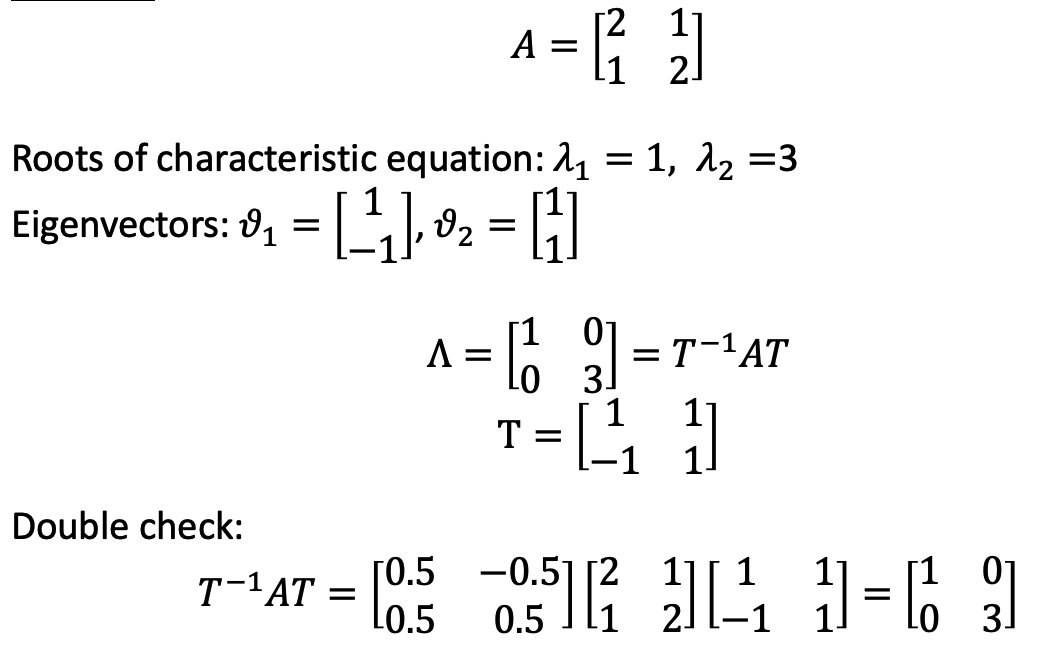
g. Matlab functions

II. Solution of linear dynamical systems

a. Definition

For sth there’s no input.

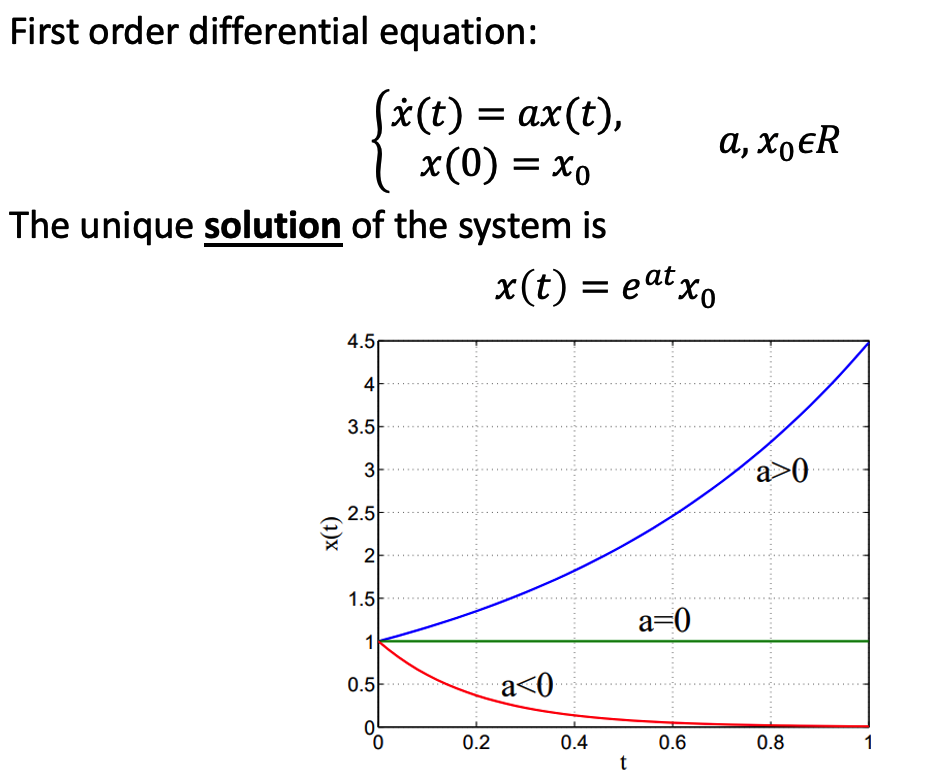
b. Example

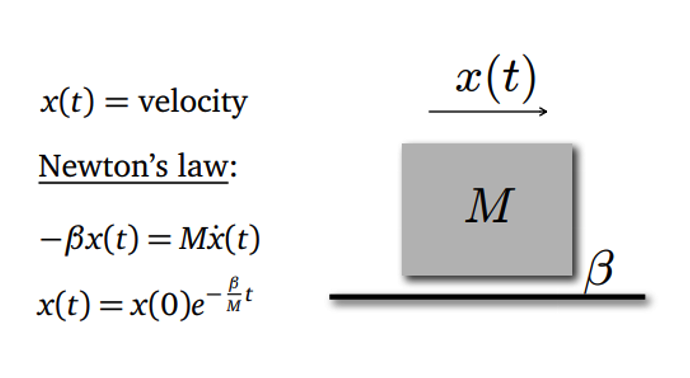
c. Definition

How do we derive the answer when input exists.

d. Lagrange’s formula

Note that we have matrix exponential here.

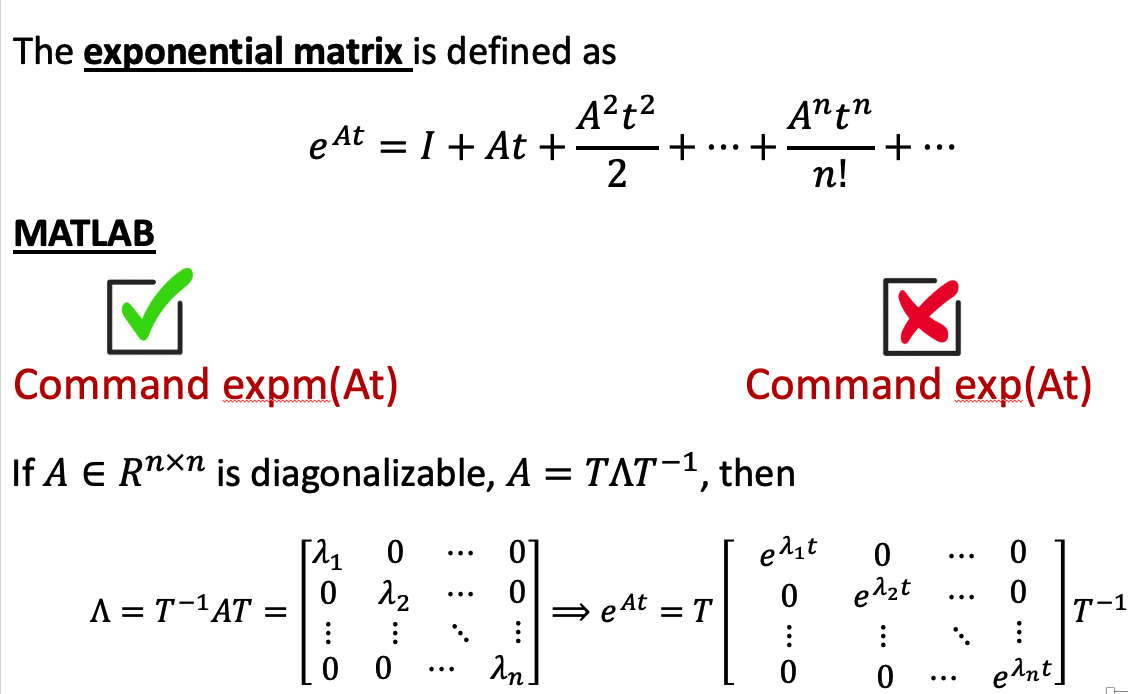
e. Example

Figure out a natural response

III. Stability

To determine if it’s stable or not without solving it.

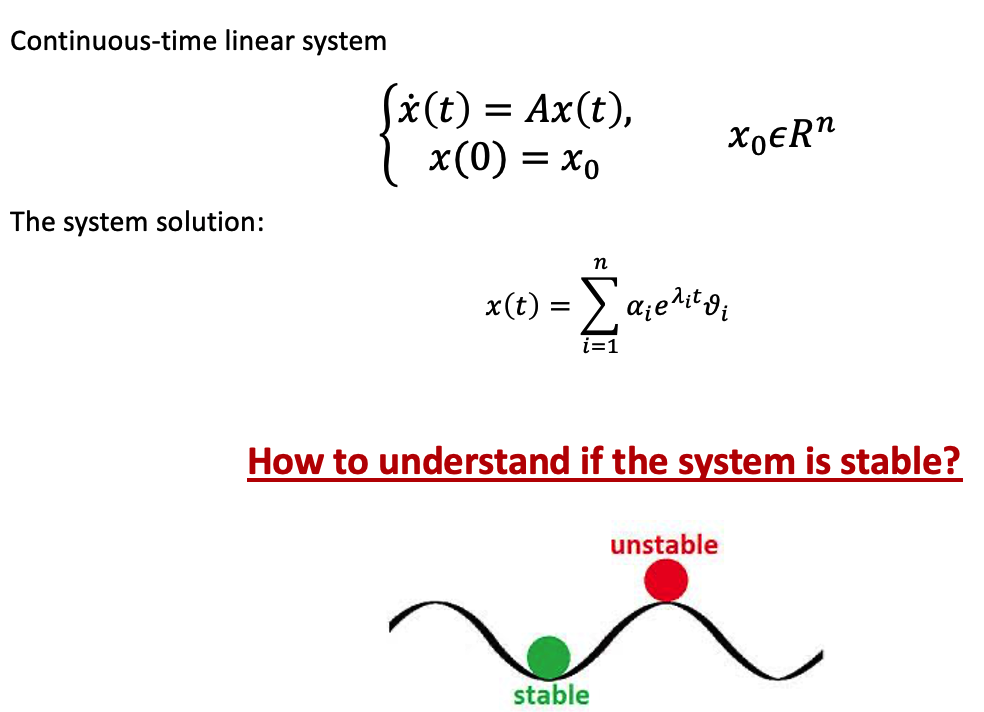
According to the eigenvalues, if there’s a positive 𝛌I, as time goes to infinity, this term goes to infinity as well. It would be unstable

If all eigenvalues are negative, the system would be stable.

a. Marginal stability

1. Neutral Type

2. Oscillatory Type

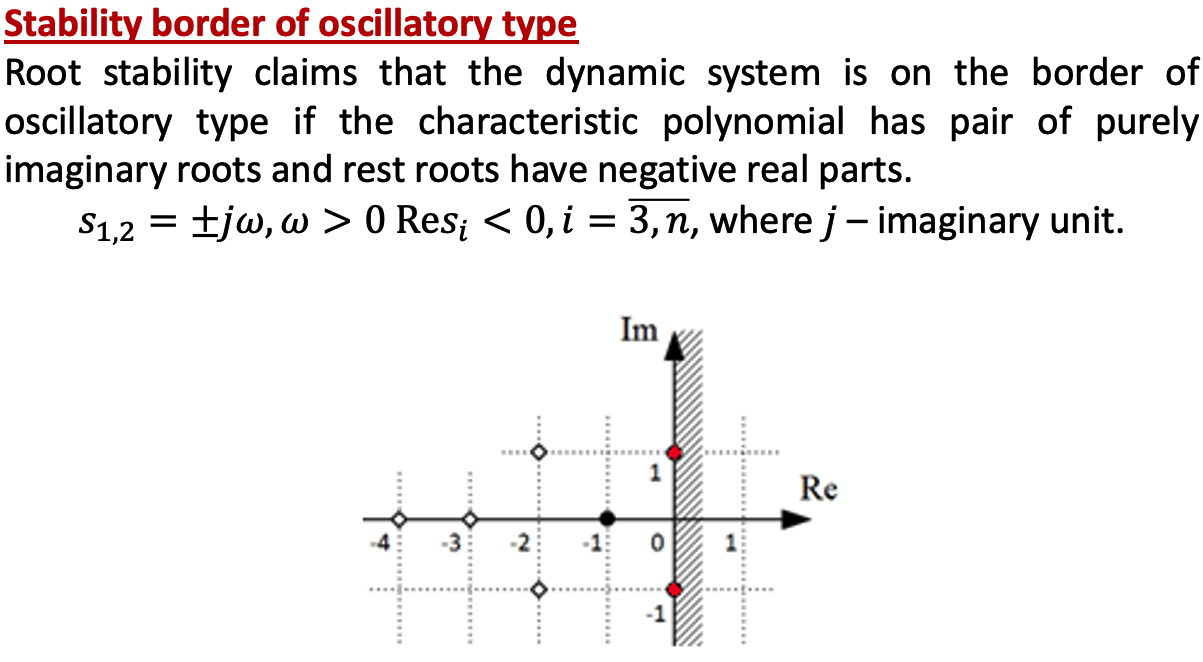
b. Asymptotic stability

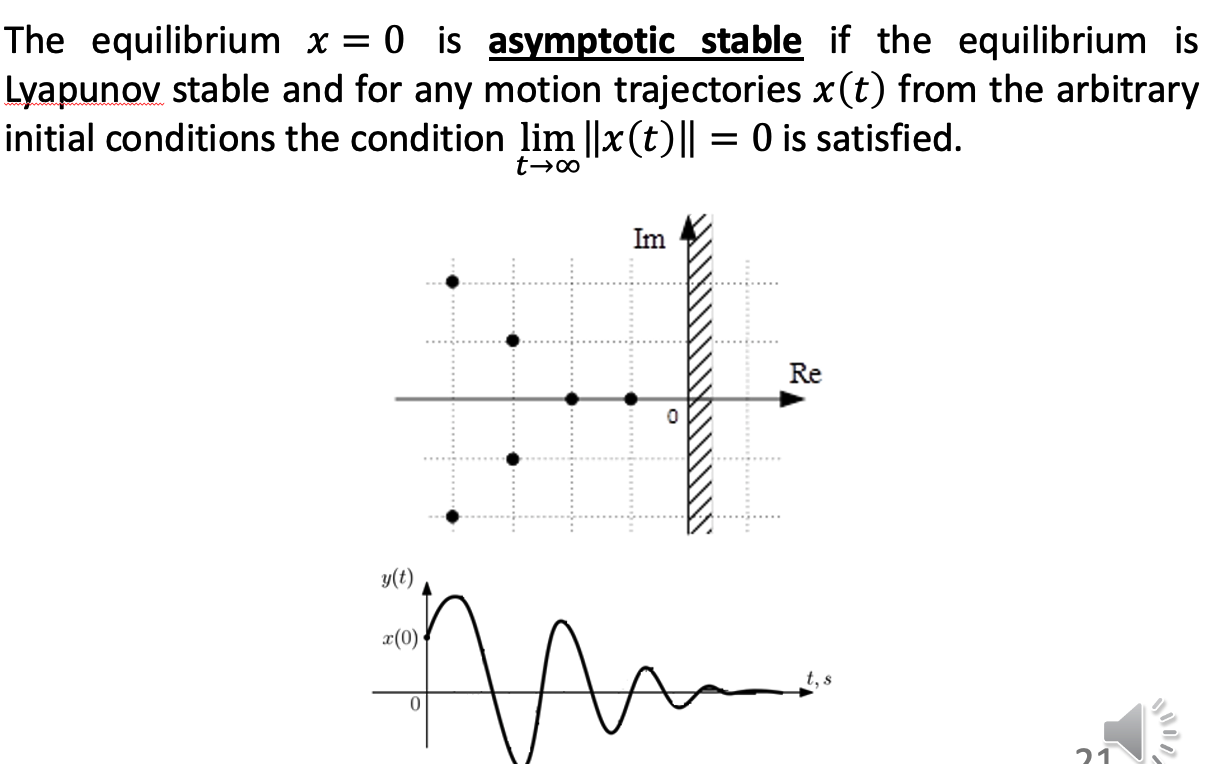
c. Qualitative behaviour of linear systems

1. node behaviour

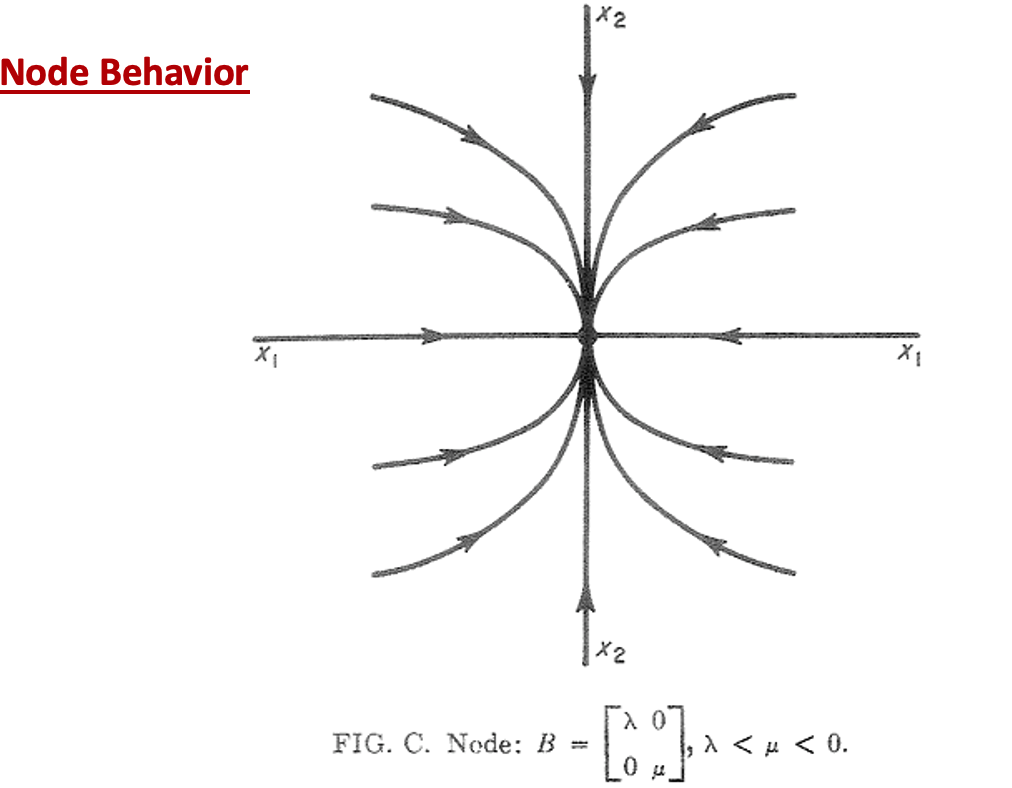
It’s a stable node behaviour (of two real negative eigenvalues), if the system is unstable, the direction of trajectory would be opposite.

2. Saddle behaviour

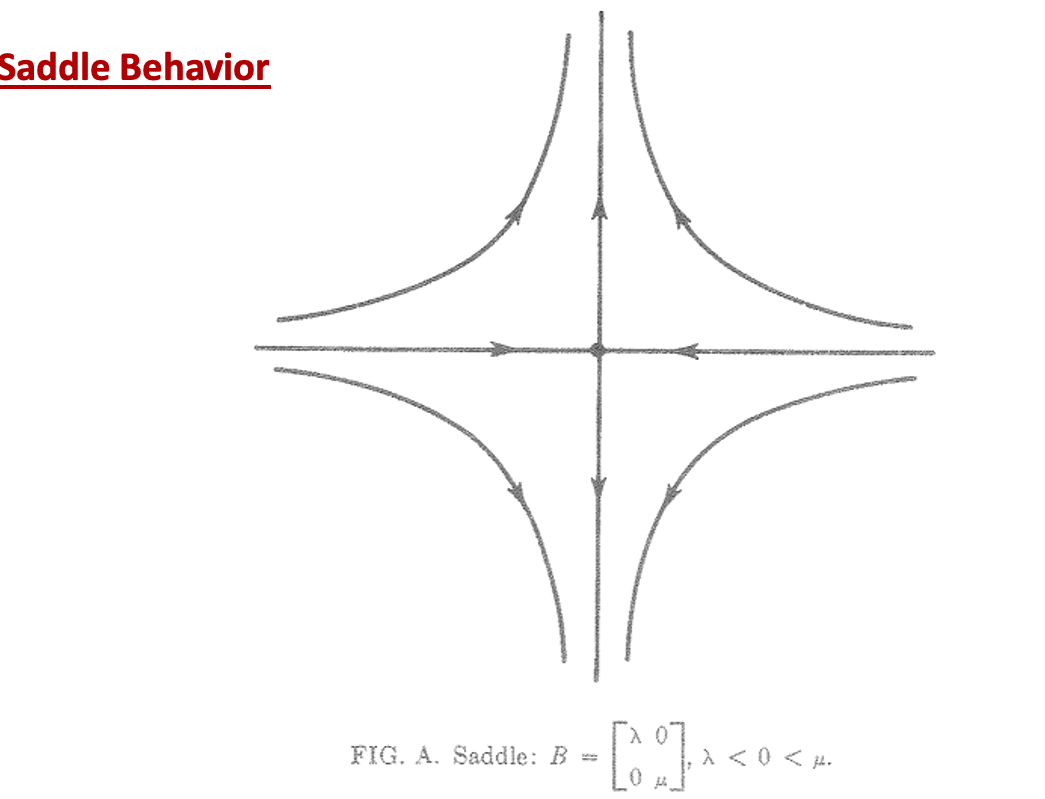
Both are real while one is negative and another is positive.

3. Spiral Behaviour (stable/unstable focus)

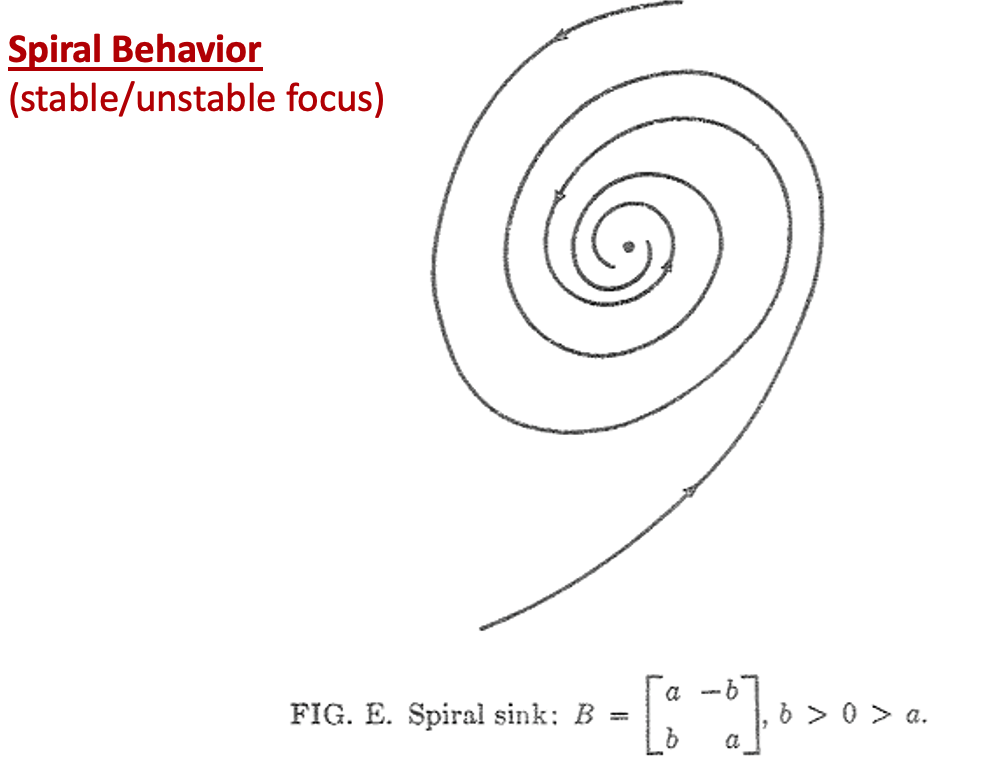
if the real parts is positive, the direction goes opposite.

4. Center behaviour

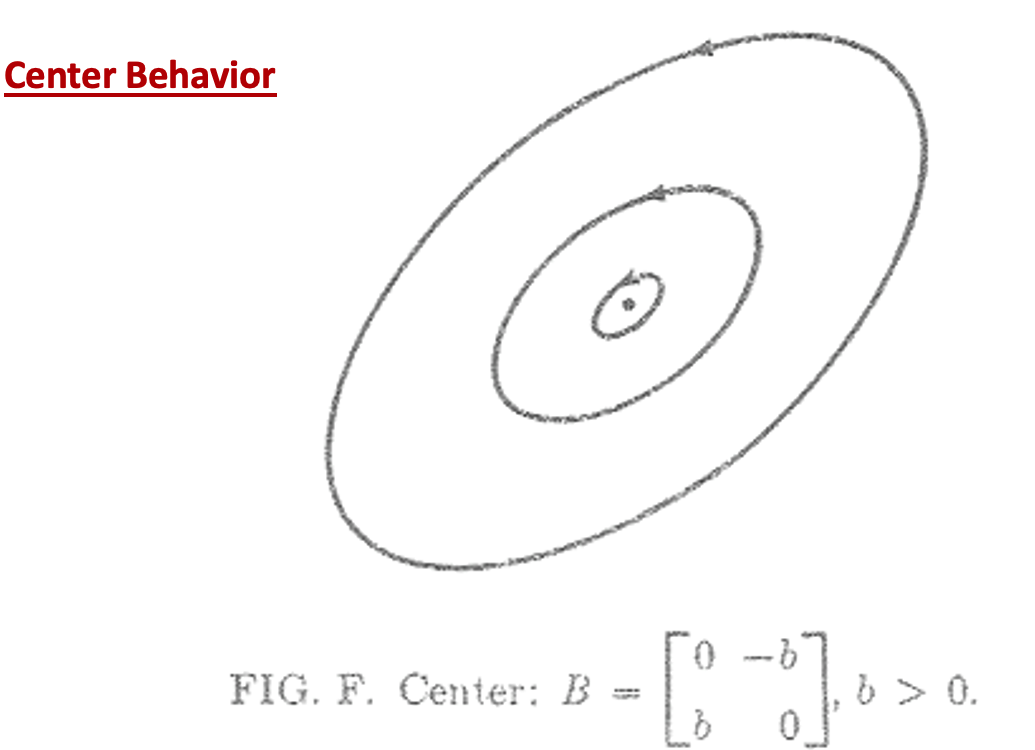
If they are on imaginary axis. the system is Lyuaponuv stable.

d. Examples