Discrete Control - Practical assignments

Comparing with merely repeat the textbook or slides, record the ideas to the problems could be more helpful.

Practice 1. Modeling of the linear discrete systems

It mainly involves the idea of a zero-order extrapolator.

A linear pulse system is such an automatic control system (ACS), which, in addition to the links described by lin- ear differential equations, includes a pulse element (PE), which converts a continuous input into a sequence of pulses.

The continuous part of the system is a set of elementary continuous links which usually describe the operation of the control object (CO). PE is a device that is part of a digital-to-analog converter.

This practice is mainly focused on tuning coefficient, the scheme is given.

ZOH

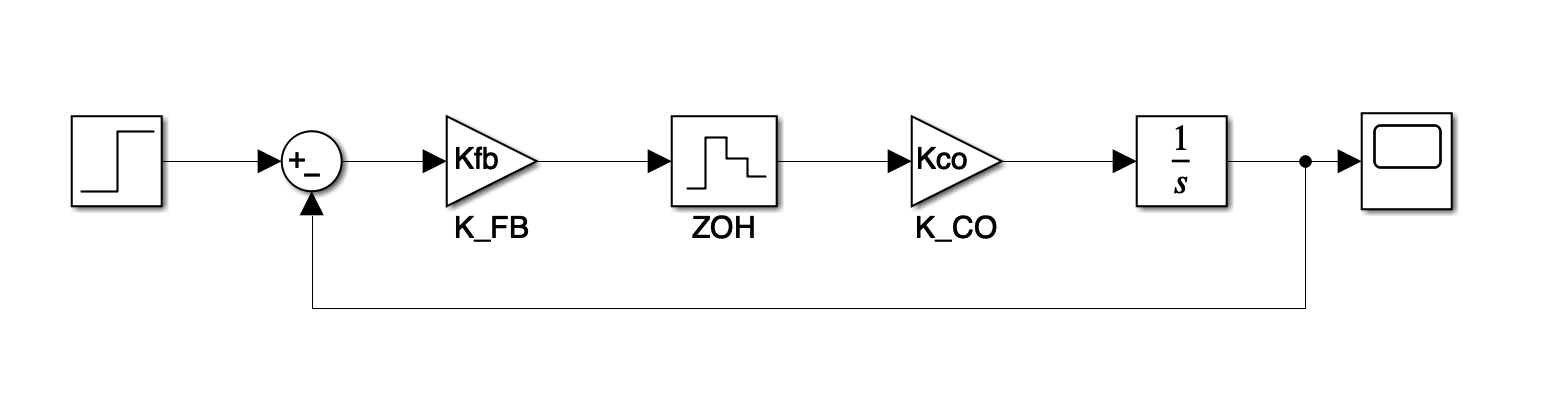
In terms of stability border, at first I thought the neutral and oscillatory represent different situations, while it turns out both two terms refer to the marginal stability, that can be regard as Lyapunov stability.

$|z|<1$ $|1-K_{FB}K_{CO}T|<1$ $|K_{FB}K_{CO}T-1|<1$

stability border $0<K_{FB}<\frac{2}{K_{CO}\cdot T}$ When $\frac{1}{K_{CO}\cdot T}\le K_{FB}\le\frac{2}{K_{CO}\cdot T}$ system has oscillations .

In the oscillation process, the larger the $K_{FB}$ is, the larger the amplitude, the slower the attenuation, the longer the transient time, before finally reach the stability boundry.

As for time optimal, and I still have problem, when determine the value,

$t^*\le-\frac{3T}{\ln\eta}$ $(1-K_{FB}K_{CO}T)\rightarrow0$ $K_{FB}\rightarrow\frac{1}{K_{CO}\cdot T}$

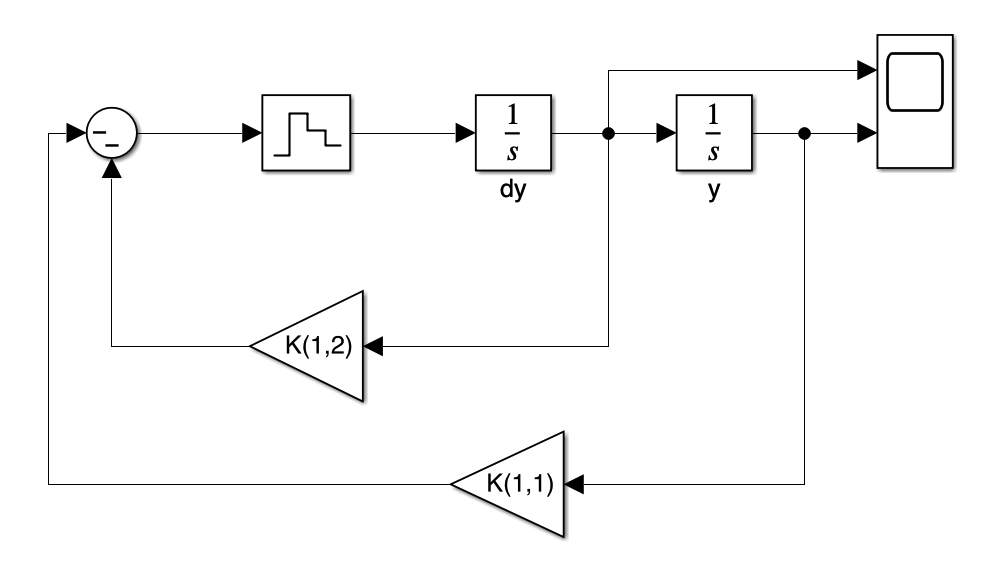
Practice 2 Second order linear discrete systems dynamic properties

This part mainly involves the discrete process of a state space model, derive corresponding feedback coefficient from given roots of character polymonial, and the plot of discrete phase portrait, other than time-consuming, there seems to be not much problem.

ZOH

Practice 3 Reference signals discrete generators

If I gotta say, the idea would be like what I learned in the modelling of nonlinear systems, but slightly different. Well, after all such representation is general. However, the idea of such generator is really smart.

Discrete Generator

$\xi_1(k+1)=\xi_2(k)$ $\xi_2(k+1)=2\cdot \xi_2(k)\cos(\omega T)-\xi_1(k)$ $g(k)=\xi_1(k)=A\sin(\omega kT)$

In my case $T=0.2,\ A=1,\ \omega=0.08$

$\xi(0)=\left[\begin{array}{c}0\\0.016\end{array}\right]$ $\xi_2(k+1)=-\xi_1(k)+1.9997\cdot \xi_2(k)$

thus

$\xi(k+1)=\left[\begin{array}{cc}0&1\\-1&1.9997\end{array}\right]\xi(k)$

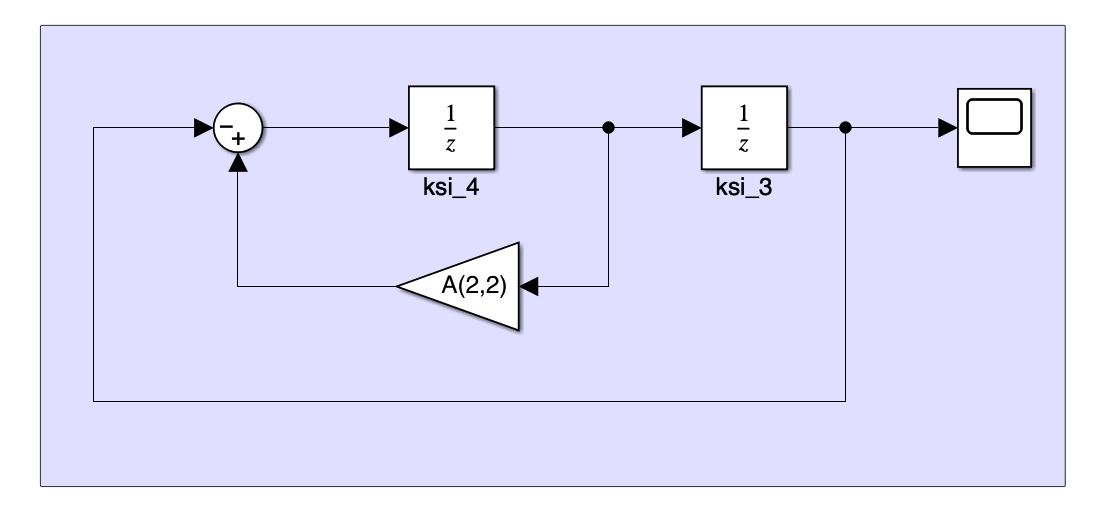
Generator

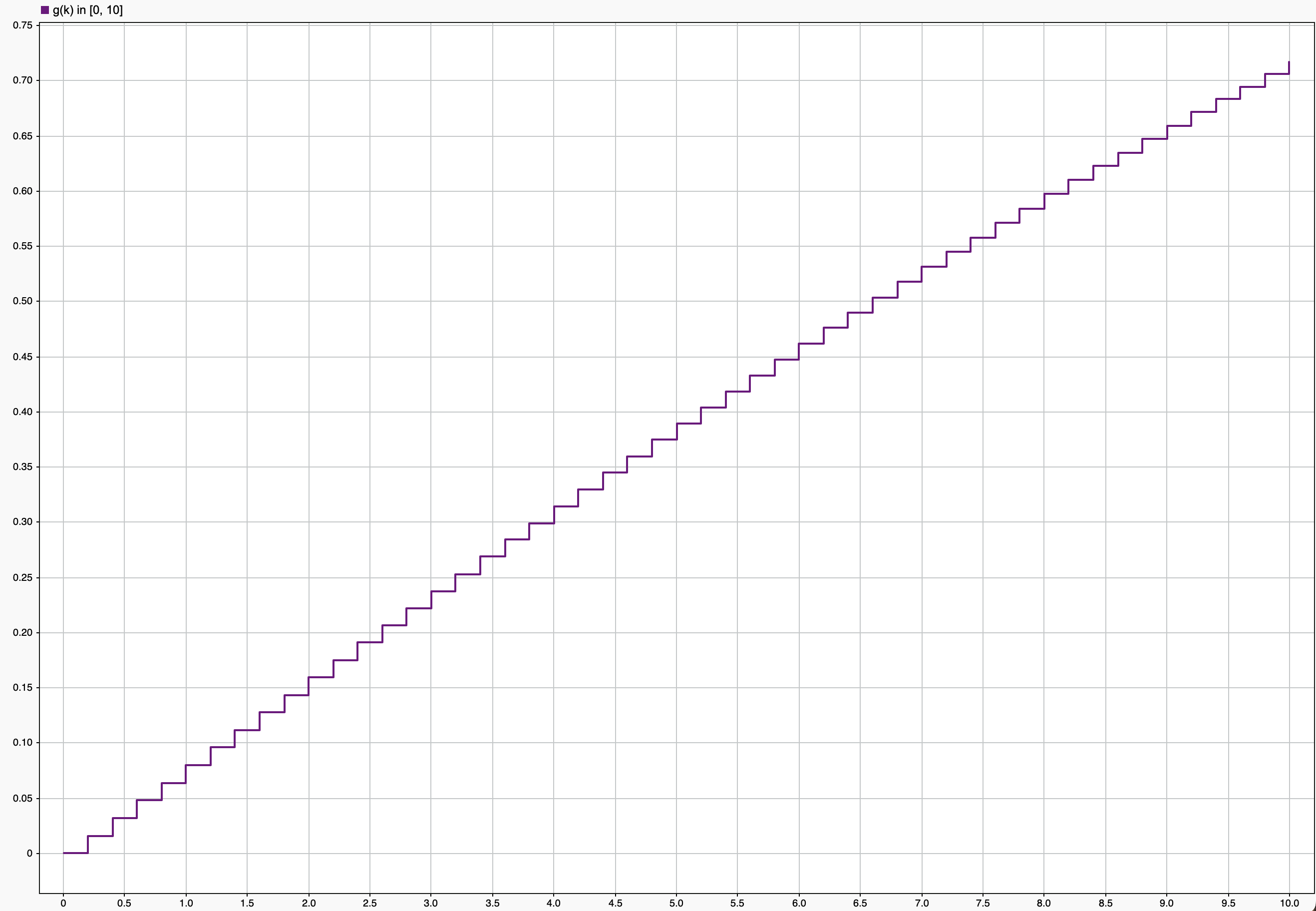
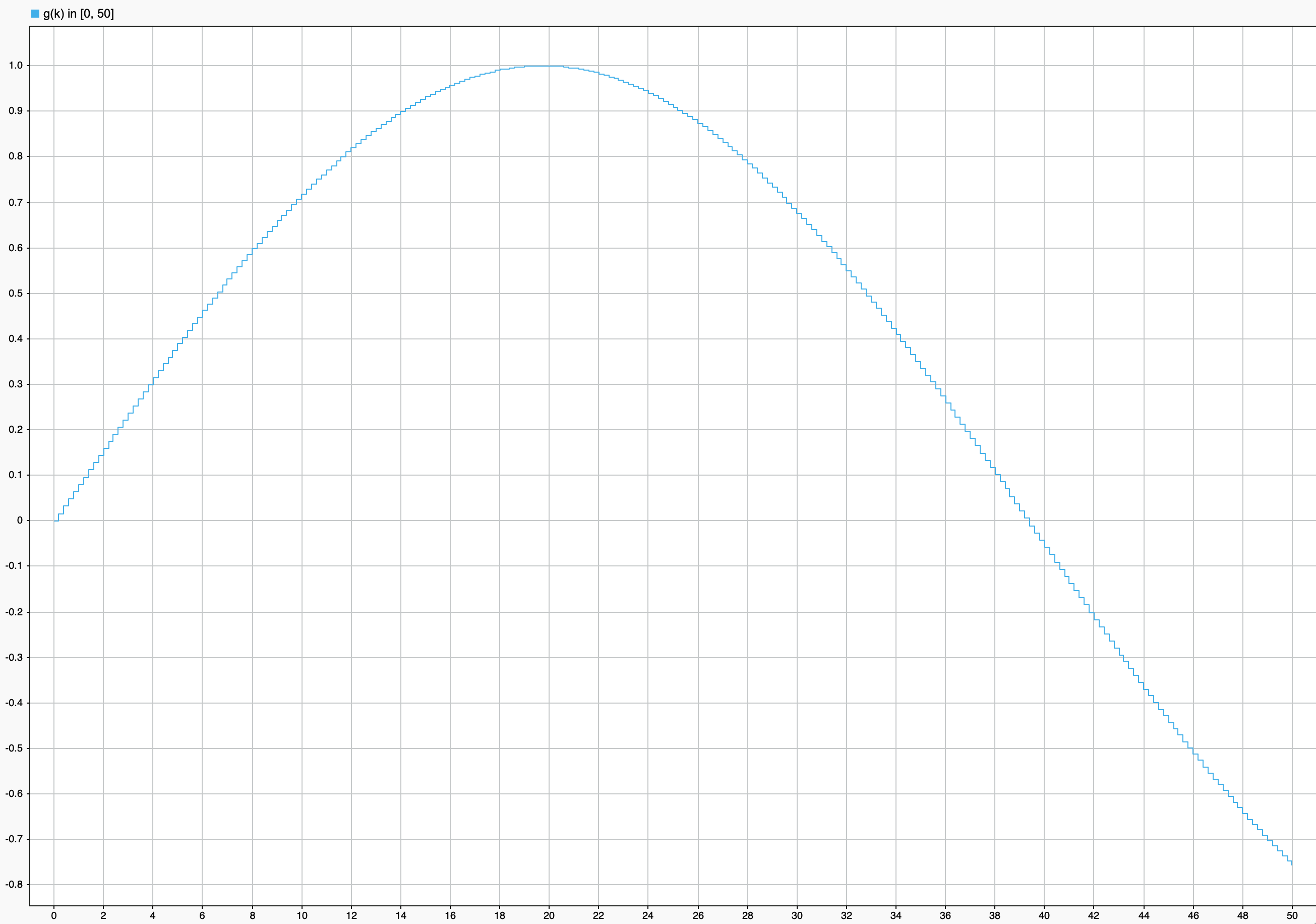
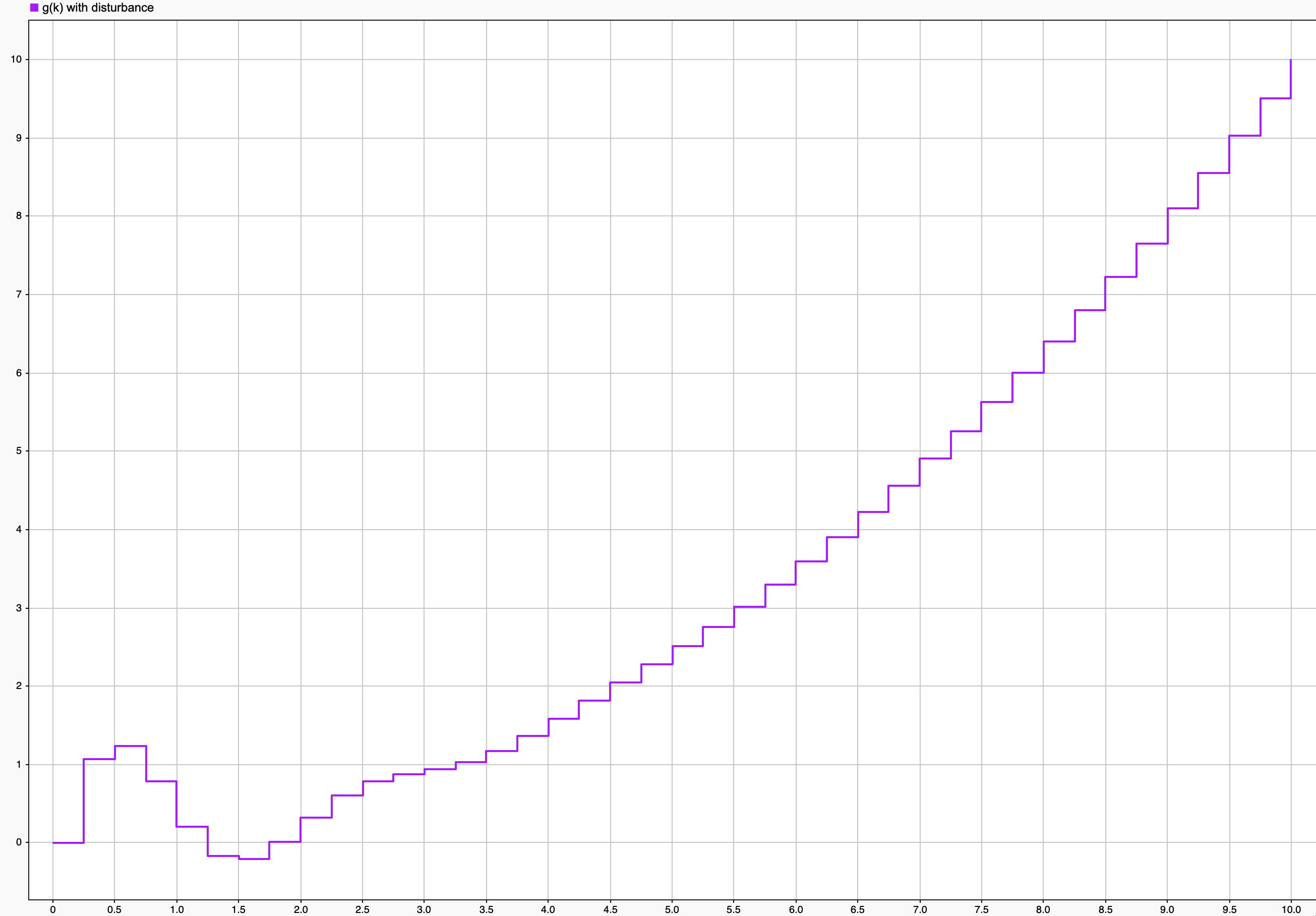
transient

External disturbance

Given

$g(k)=2e^{-kT}\sin(3kT)+0.1(kT)^2$

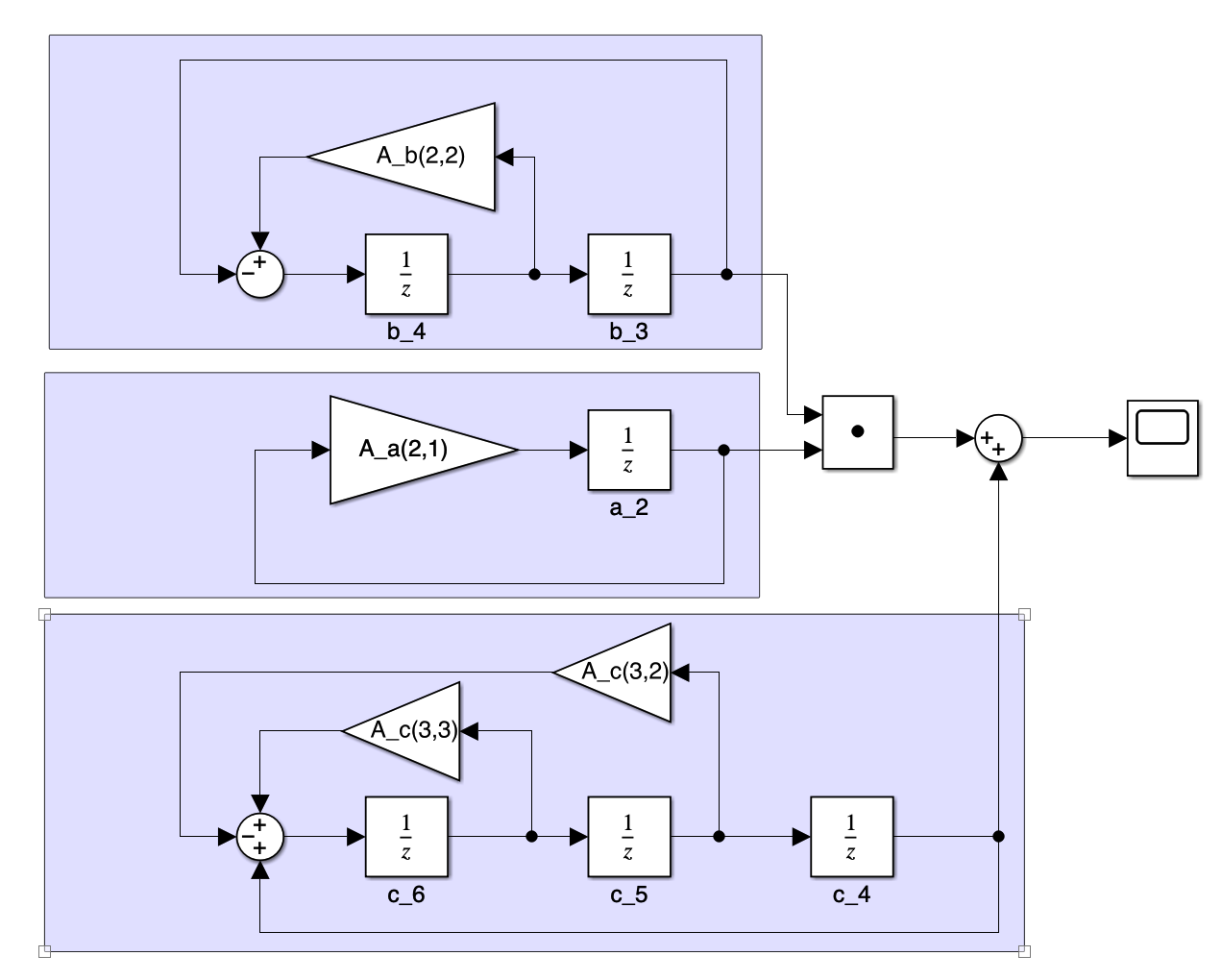
The Idea is to create three generators

$g_1(k)=2e^{-kT}$ $g_2(k)=\sin(3kT)$ $g_3(k)=0.1(kT)^2$ $g(k)=g_1(k)g_2(k)+g_3(k)$

First generator

$a_1(k)=g_1$ $a_2(k)=a_1(k+1)=2\cdot e^{-kT}\cdot e^{-T}=a_1(k)\cdot e^{-T}$ $a(k+1)=\left[\begin{array}{cc}0&1\\e^{-T}&0\end{array}\right]a(k)$

Second generator

$b_1(k)=g_2(k)$ $b_2(k)=b_1(k+1)=\cos(3T)\cdot\sin(3kT)+sin(3T)\cdot \cos(3kT)$ $b_3(k)=b_2(k+1)=2\cdot b_2(k)\cdot\cos(3T)-b_1(k)$ $b(k+1)=\left[\begin{array}{cc}0&1\\-1&2\cos(3T)\end{array}\right]b(k)$

Third generator
$c_1=g_3(k)$ $c_2(k)=c_1(k+1)=0.1((k+1)T)^2=0.1((kT)^2+2kT^2+T^2)=\\c_1(k)+0.2kT^2+0.1T^2$ $c_2(k)-c_1(k)=0.2kT^2+0.1T^2$ $c_3(k)=c_2(k+1)=c_1(k+1)+0.2(k+1)T^2+0.1T^2\\=c_2(k)+0.2kT^2+0.3T^2$ $c_3(k)-c_2(k)=c_2(k)-c_1(k)+0.2T^2$ $c_4(k)=c_3(k+1)=c_3(k)+c_2(k)-c_1(k) +2（c_3(k)-2c_2(k)+c_1(k)）\\=3c_3(k)-3c2(k)+c_1(k)$ $c(k+1)=\left[\begin{array}{ccc}0&1&0\\0&0&1\\1&-3&3\end{array}\right]c(k)$
Then the left synthesis would be easy.

Practice 4. Synthesis of the discrete stabilizing control algorithms

Course Work

State-space representation

$K_2 = 425.00\ \\ T_2 = 0.12\ \\ K_3 = 0.25$ $W_2 = \frac{K_2}{T_2 p+1}\ \\W_3 = \frac{K_3}{p}$ $\left\{\begin{array}{l}\dot{x}_1=K_3 \cdot x_2\\\dot{x}_2=\frac{1}{T_2}(-x_2+K_2)\end{array}\right.$

Transform to state-space form

$\dot{X}=A_HX+B_HU,\\Y=CX$

where

$X=\left[\begin{array}{c}x_1\\x_2\end{array}\right],\ A_H=\left[\begin{array}{cc}0&K_3\\0&-\frac{1}{T_2}\end{array}\right],\ B_H=\left[\begin{array}{c}0\\\frac{K_2}{T_2}\end{array}\right],\ C=\left[\begin{array}{cc}1&0\end{array}\right]$

Skip the discretization process and the representation (for convenience), to note $T=0.003$

$A_d=e^{A_H\cdot T},\ B_d=(\sum_{i=1}^\infty\frac{T^i A_H^{i-1}}{i!})B_H$

Systhesis PI controller

Old fashioned modal control (which again, I didn’t find any relavent info online, maybe Russians prefer to call it in this way)

First construct augmented matrix, as there’s no disturbance, the term is not written.

$v(k)$ is the integral term, and $g(k)$ represents reference signal

$u(k)=K_{FB}\cdot e(k)$

And naturally for integral,

$v(k+1)=v(k)+e(k)=v(k)+g(k)-x_1(k),\ v(0)=0$ $u(k)=K_p\cdot e(k)+K_i\cdot v(k)-K_2\cdot x_2(k)\ \\=K_p\cdot g(k)+K_i\cdot v(k)-(K_p\cdot x_1(k)+K_2\cdot x_2(k))$ $x(k+1)=A_d\cdot x(k)+B_d\cdot u(k)$

Perform augmentation,

$\left[\begin{array}{c}v(k+1)\\x(k+1)\end{array}\right]=\left[\begin{array}{cc}1&-C\\0&A_d\end{array}\right]\left[\begin{array}{c}v(k)\\x(k)\end{array}\right]+\left[\begin{array}{c}0\\B_d\end{array}\right]+\left[\begin{array}{c}1\\0\end{array}\right]g(k)$ $u(k)=K_p g(k)-\bar{K}\bar{x}(k)$

Choose standard binomial polynomial of the third degree as reference

$(\lambda+\omega_0)^3, t_\Pi \cdot \omega_0=8.5$

(required more investigation here, as this number is different from the content in documentation used before)

$\lambda_{1,2,3}=-\frac{t_\Pi \cdot \omega_0}{t_{desire}}$ $\Gamma_H=\left[\begin{array}{ccc}\lambda&1&0\\0 &\lambda&1\\0&0&\lambda\end{array}\right]$ $H=\left[\begin{array}{cc}1&0&0\end{array}\right]\ \\ G_d=e^{\Gamma_H\cdot T}$ $-\bar{A}\cdot M+G_d\cdot M+\bar{B}\cdot H=0$

solve the sylvester equation with sylv(-A,G,B*H) or lyap(-A,G,B*H)

and

$\bar{K}=HM^{-1}$

Obtain

$K=\left[\begin{array}{cc}-K_i&K_p&K_2\end{array}\right]$

The rest should be really simple like making simulations and evaluations. (e.g. lsiminfo)

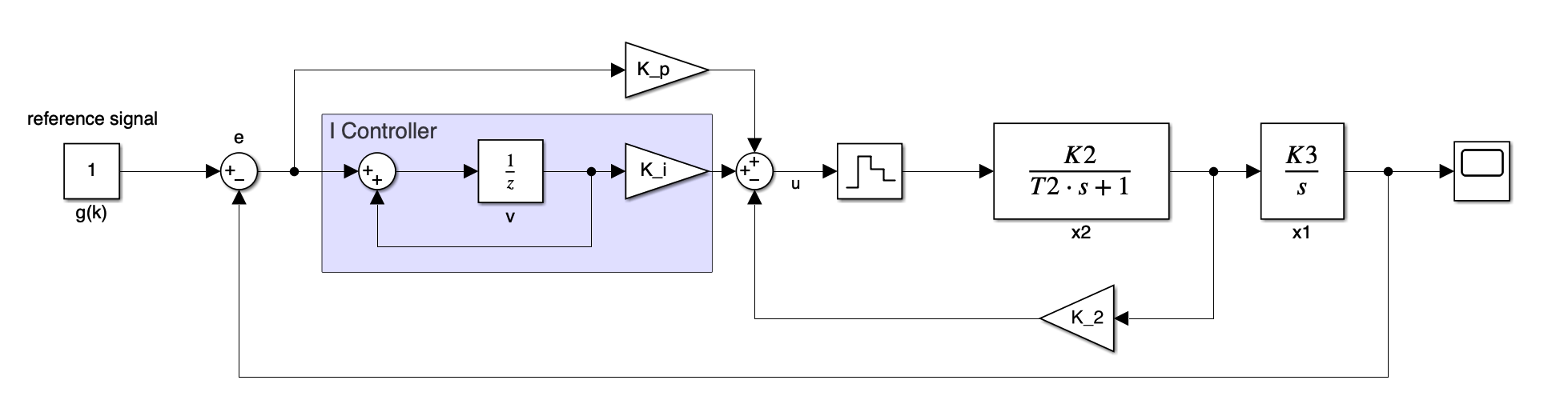
SynScheme

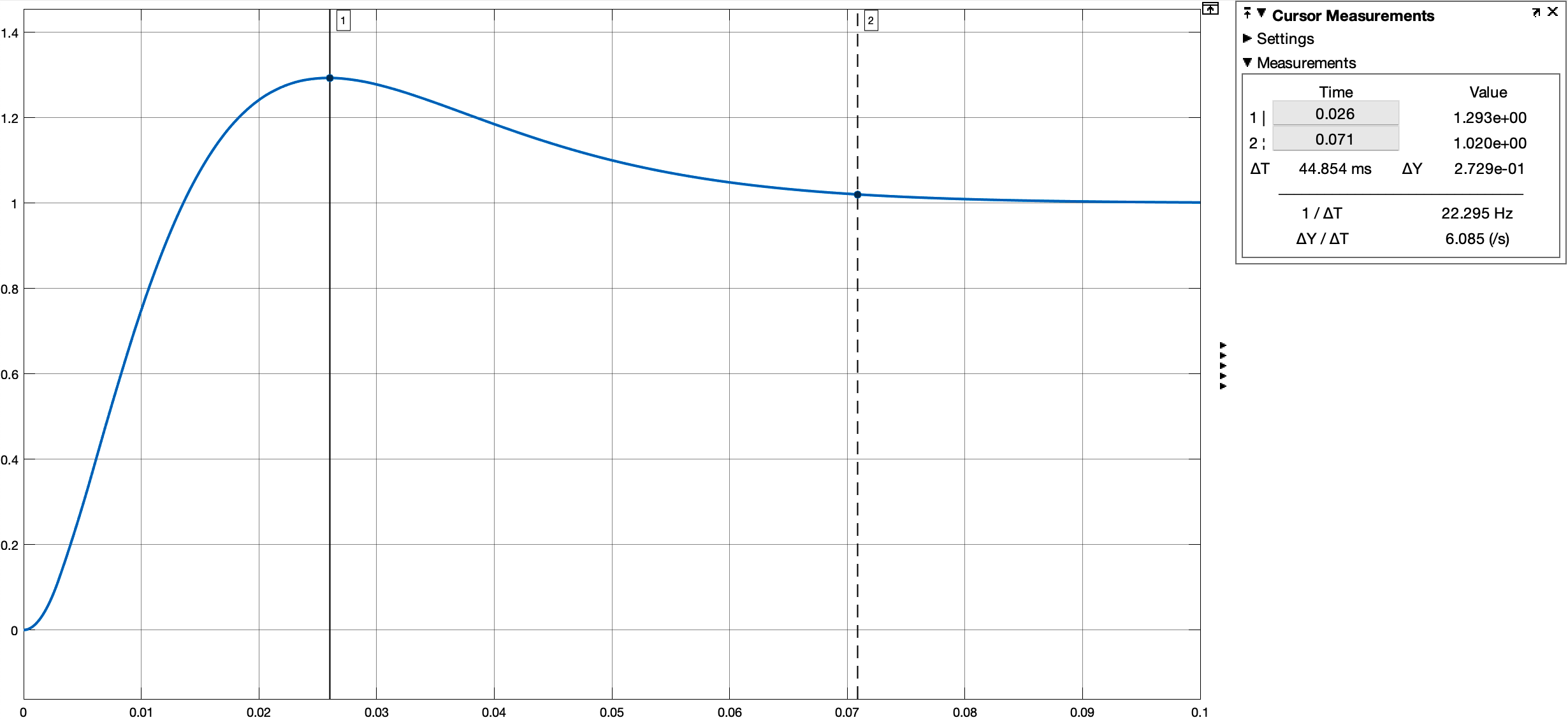
At first, I didn’t realize that the implementation of I regulator requires an additional states, so the derived M looks really weird, but now I see.

Oh my, the report writing… it’s killing me.

Practice 5.

Practice 6.

Design complete dimension observer:

$\left\{\begin{array}{l} \hat{x}(k+1)=A_d\cdot \hat{x}(k)+L(y_m(k)-C_m\cdot \hat{x}(k))+B_d\cdot u(k)\\ u(k)=K_d\cdot \hat{x}(k) \end{array}\right.$

Consider representing the error of observer:

$\tilde{x}(k)=x(k)-\hat{x}(k)$ $\tilde{x}(k+1)=A_d\cdot \tilde{x}(k)-L\cdot C_m\cdot \tilde{x}(k)=F_z\cdot \tilde{x}(k)$ $F_z = A_d-L\cdot C_m$

P3

$1+G_R(z)G_P(z)=0$

where $G_R(z)$ is the controller $\frac{Q}{P}$, and the latter is the process $\frac{B}{A}$

$(z-z_{a1})(z-z_{a2})\dots(z-z_{a(m+2+d)})=0$ $m=2-d,\ d=0$ $P(z^{-1})=(1-z^{-1})(1+\gamma_1 z^{-1})$ $A(z)=(z-z_1)(z-z_2)=z^2-(z_1+z_2)z+z_1z_2$ $A(z^{-1})=1+a_1z^{-1}+a_2z^{-2}$