Yup?

Table of Contents

1. Lec 3 Laplace Transform and transfer functions
   1. I. Formal Definition
   2. II. List of Laplace Transforms
      1. 1. 𝜹 function
      2. 2. 1
      3. 3. Polynominal function
      4. 4. Expoential fucntion
      5. 5. General version.
      6. 6. Sin and Cos function
      7. 7. SHM with exponential
      8. 8. Normal sin func
   3. III. Main properties.
      1. 1. The reasons we love them.
   4. IV. Solving differential equations with Laplace transform
   5. V. Natrual and forced response
      1. 1. Case Analysis
      2. 2. Example
   6. VI. Transfer function of dynamical system
      1. 1. Dynamical system
   7. VII. Transfer function and stabiliy
      1. 1. Impulse Response and step respose
         1. a. Impulse response
         2. b. Easy to check
         3. c. Step response
   8. VIII. General forced response
   9. IX. Steady-state value
      1. 1. Final value thorem
         1. a. Example
         2. b. Anti-example
   10. X. Closed-loop system
       1. 1. Two basic type
       2. 2. Example
          1. a. eg1
          2. b. eg2

Lec 3 Laplace Transform and transfer functions

I. Formal Definition

It’s such a integral. (Actually can be left without remembring it, but it will be better to be in head of course.)

t is eliminated here.

Function of time is changed into function of frequency, sort of. Generlized.

II. List of Laplace Transforms

1. 𝜹 function

​ It’s not actually a function, which is called distribution, or a generlized function. It can be regarded as zero except that it is infinity when t equals zero.

2. 1

​ It’s a step function. (seeing definition not here, it’s simple)

3. Polynominal function

​ Two case before is the speical case for this.

4. Expoential fucntion

​ One of the most important one.

5. General version.

​ Generlized case 3 and 4. Good assumption.

6. Sin and Cos function

​ Images in the laplace domain. Important as well. Same denominator.

7. SHM with exponential

​ Generlized case 4 and 6.

8. Normal sin func

​ Not important one.

They look like more simple than the original, you get some fractional and rational fucntion.

III. Main properties.

1. The reasons we love them.

The green parts disappear (only when at inital moment, it is zero).

IV. Solving differential equations with Laplace transform

• Note that we consider that it happens in the positive moments, and when it comes to negative ones, they have 0.
• Capitial Y is sth we don’t know yet, and we denote it in such way.

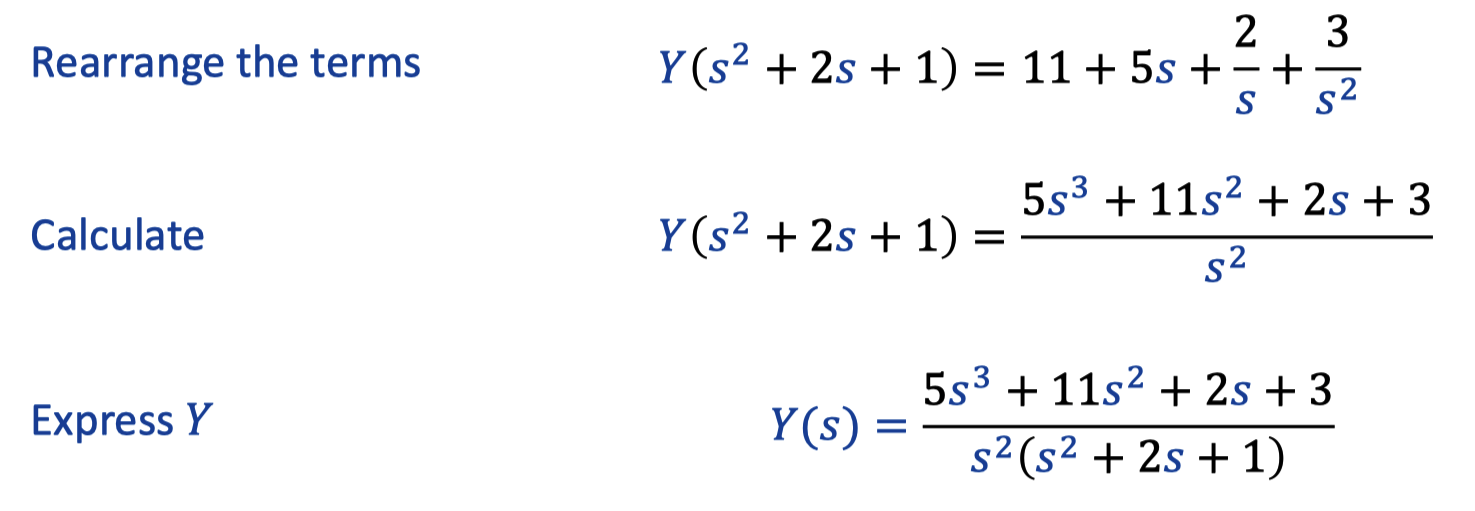
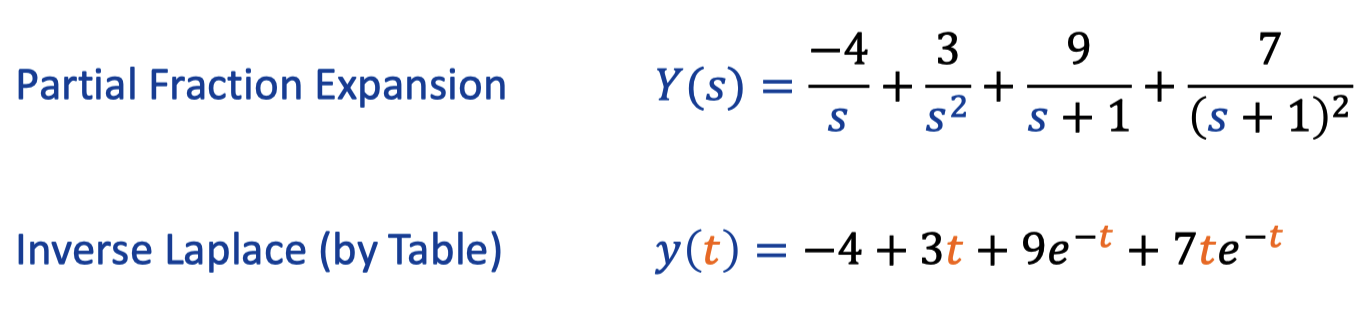
V. Natrual and forced response

1. Case Analysis

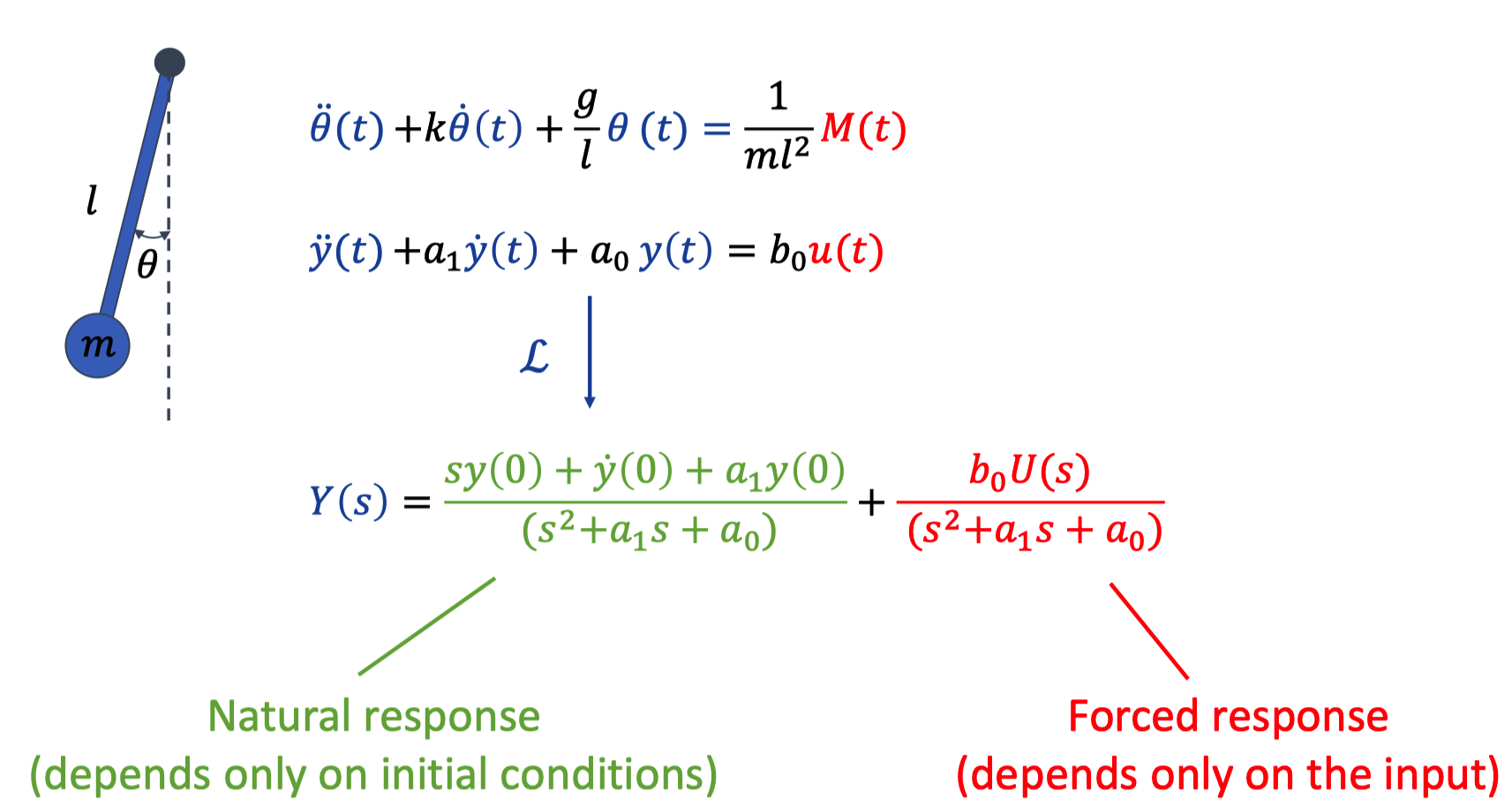
After inverse Laplace

• Word ‘Eigen’ is similiar to characteristic

2. Example

VI. Transfer function of dynamical system

1. Dynamical system

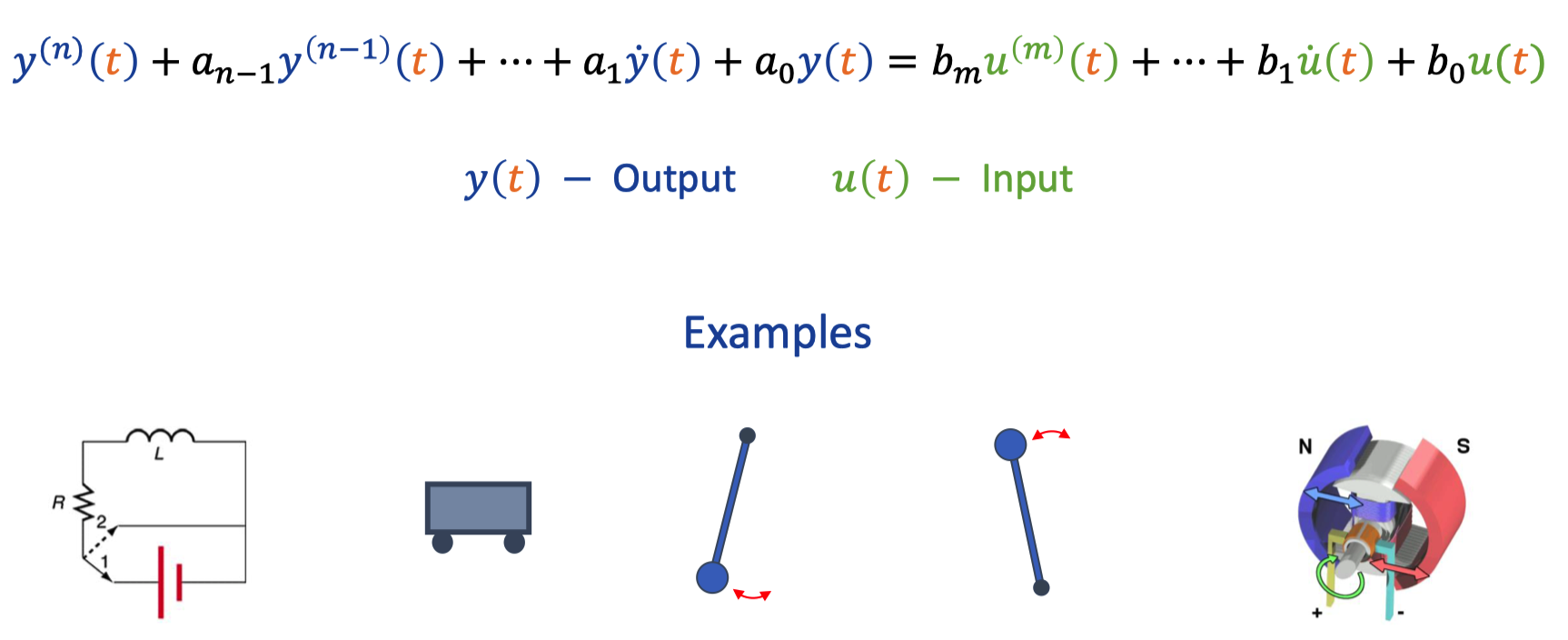
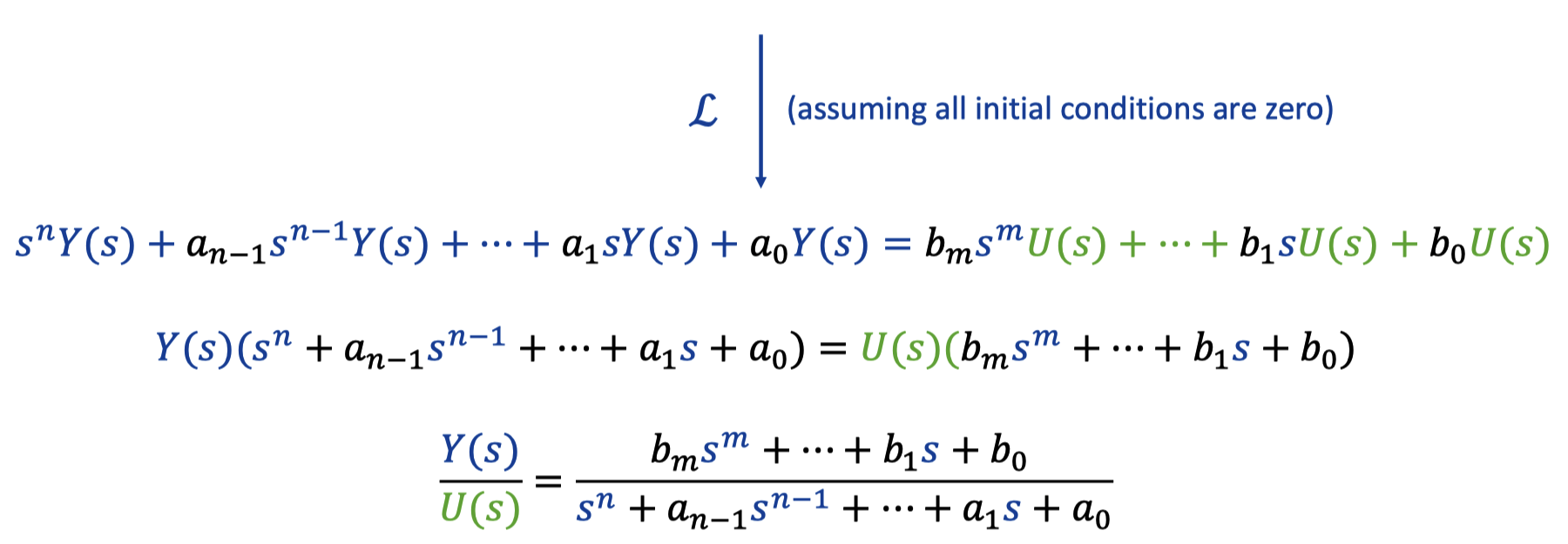
Transfer function - Ratio between Laplace Images of an Output and an Input of a linear system.

• Assuming all inital conditions are zero.
• Do not depend on particular choice of input.

It captures the behaviour of the system with a respond to every possible input.

Way of representing a system.

VII. Transfer function and stabiliy

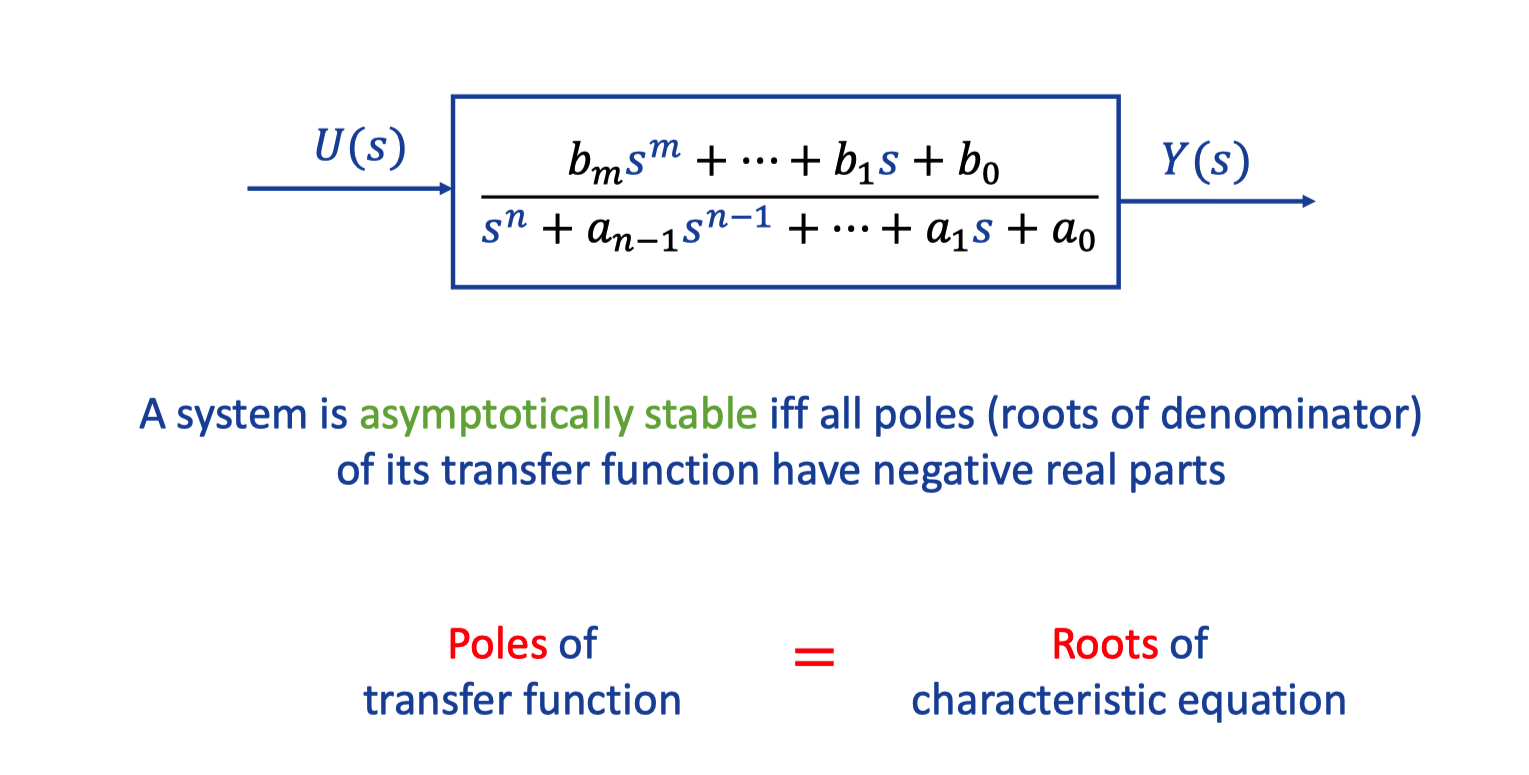
• Zeros are the roots of numerator

1. Impulse Response and step respose

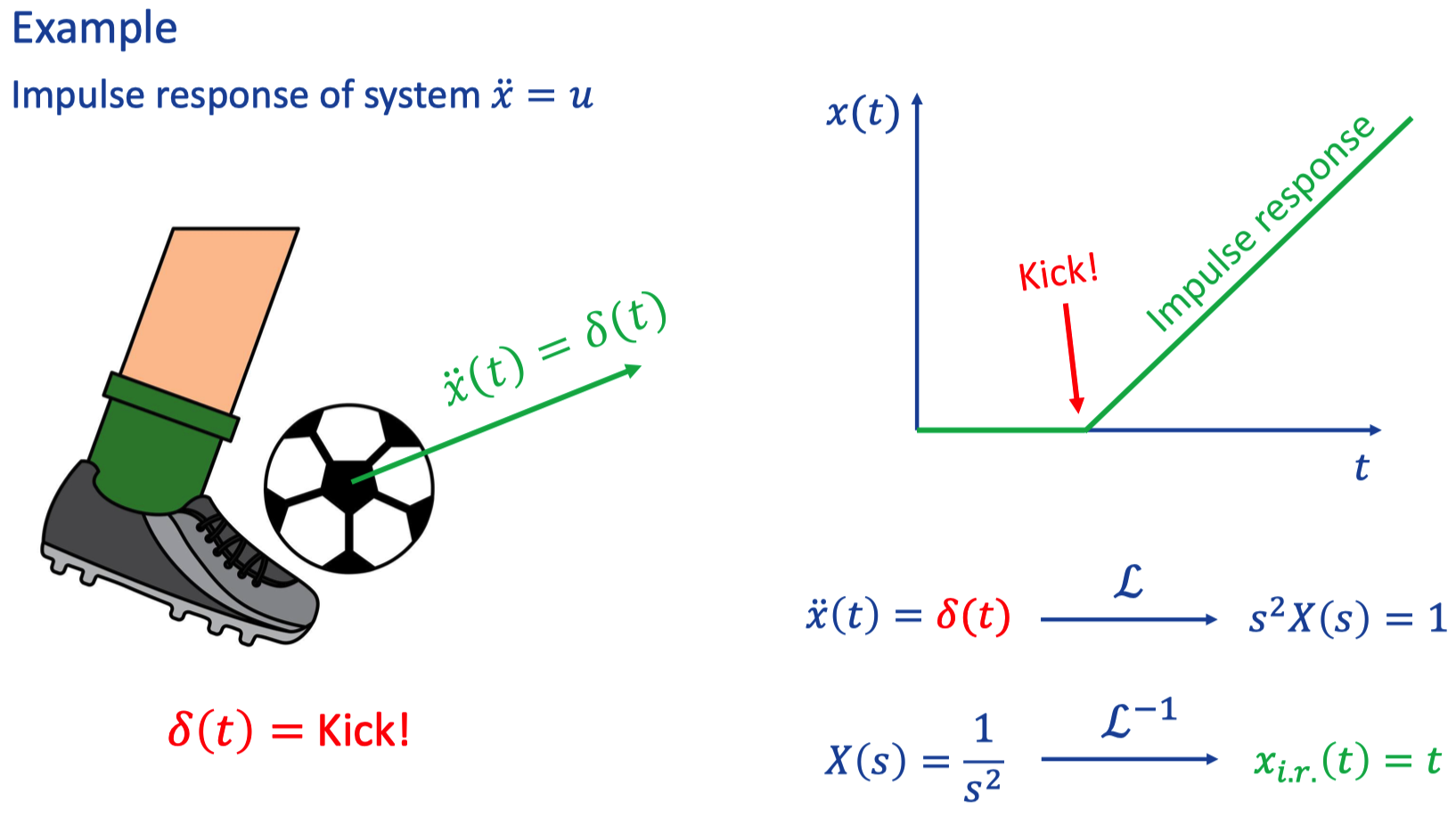
a. Impulse response

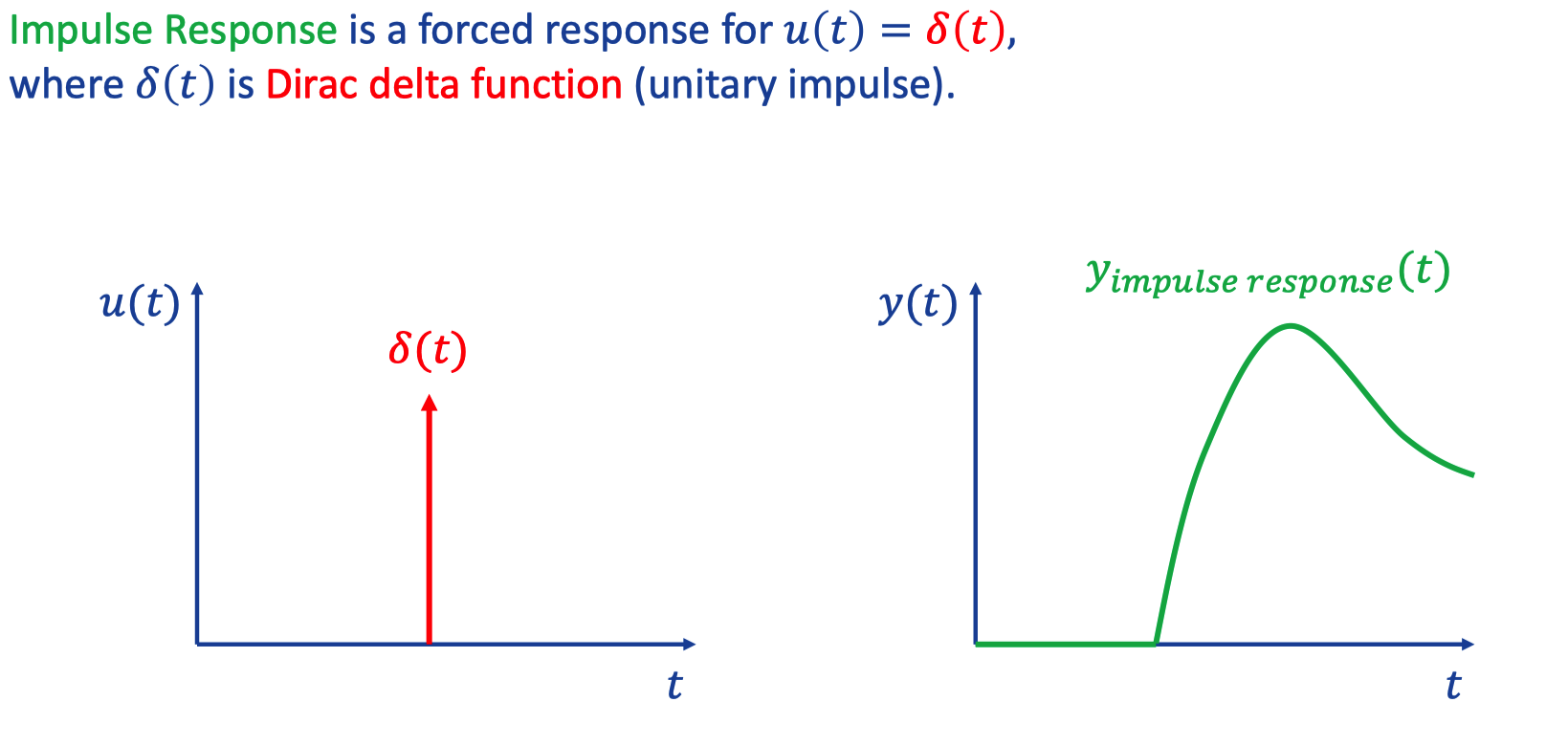
The integral of 𝝳(t) equals to 1. (Fiction function)

Eg. To hit a Pendulum | Ball.

b. Easy to check

Laplace tranform of impulse function equals to the transfer function

$\mathcal{L}\{y_{impulse response}(t)\} = W(s)$

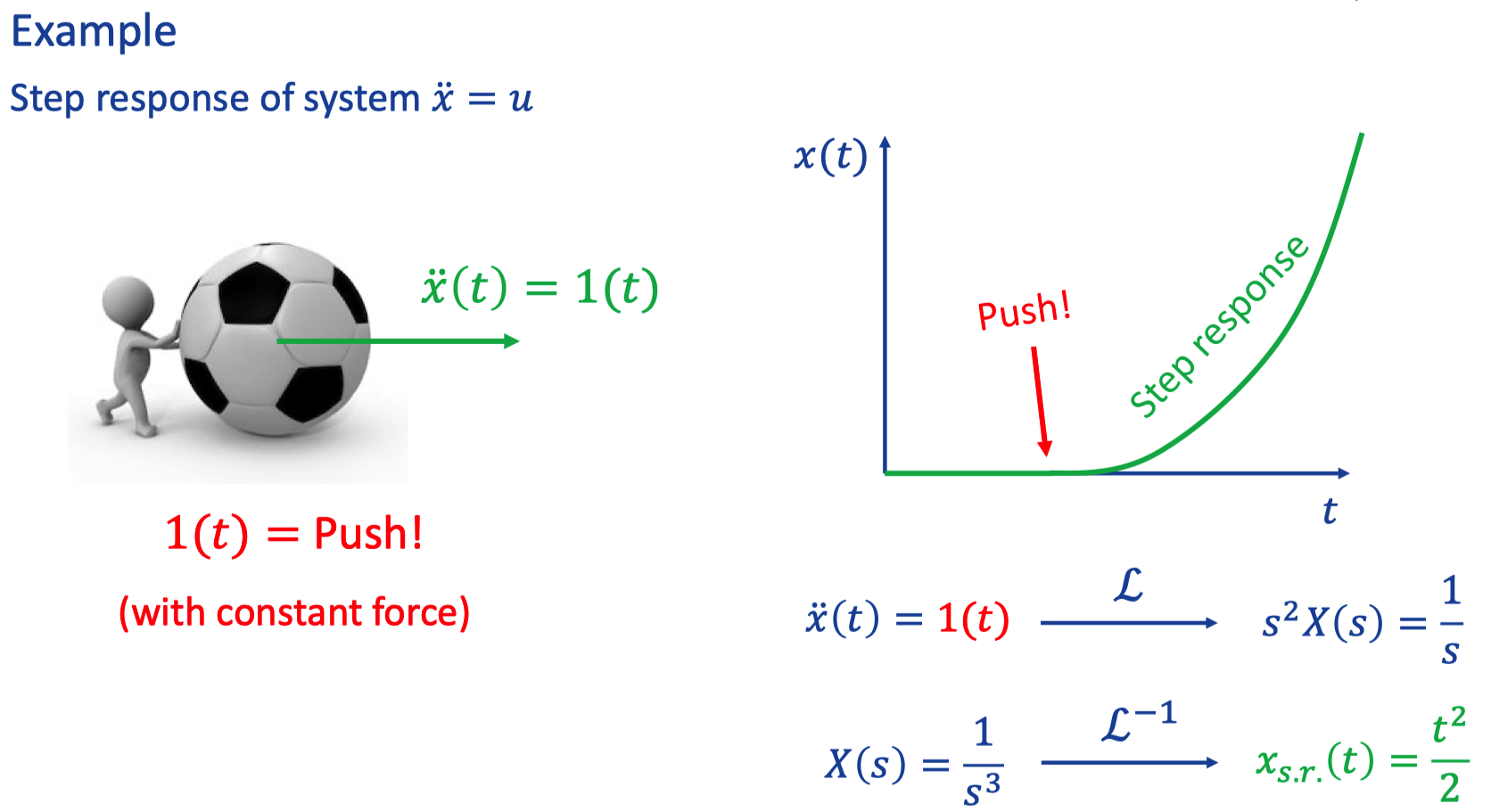
c. Step response

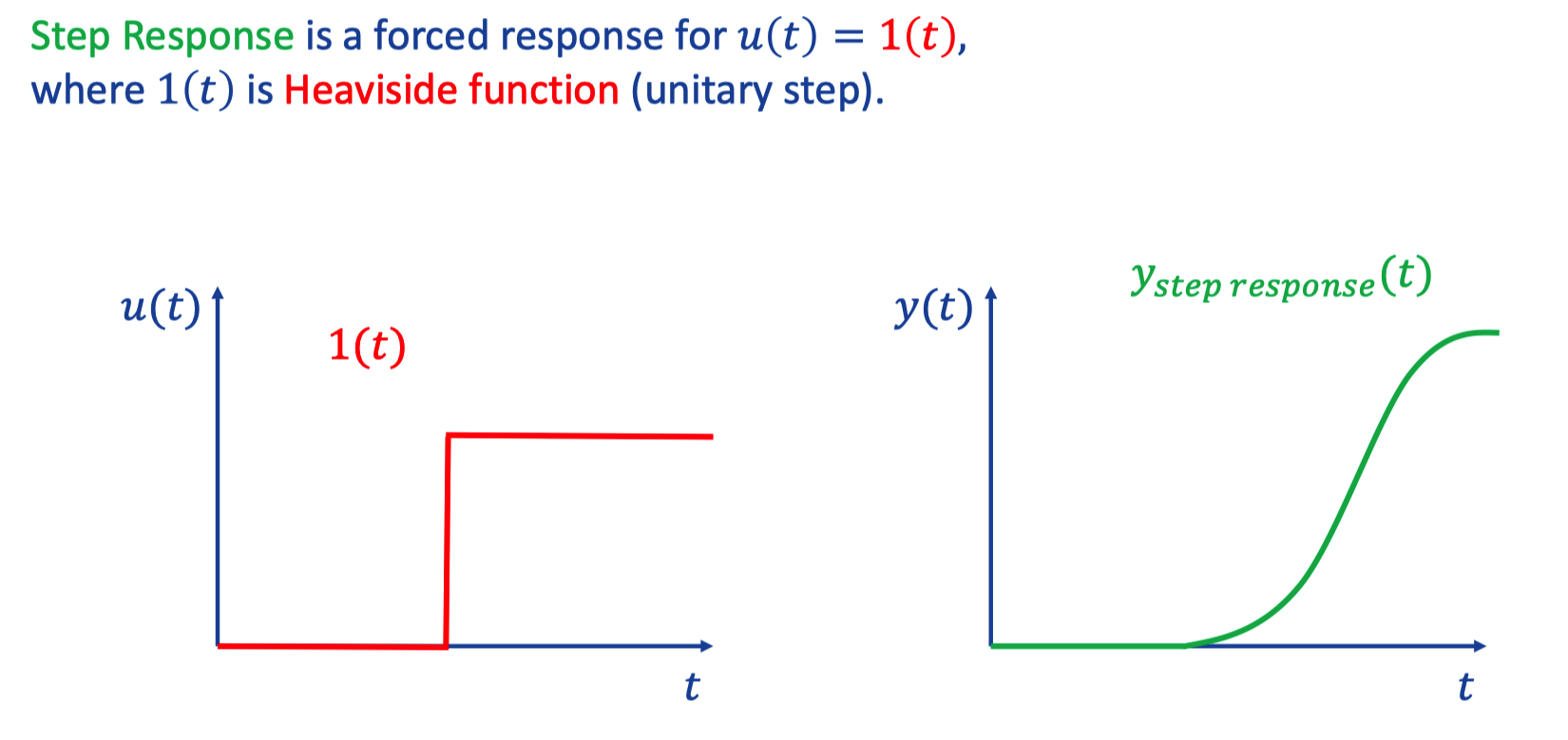
• The Heaviside step function, or the unit step function, usually denoted by H or θ (but sometimes u, 1 or 𝟙), is a discontinuous function), whose value is zero) for negative arguments and one) for positive arguments.

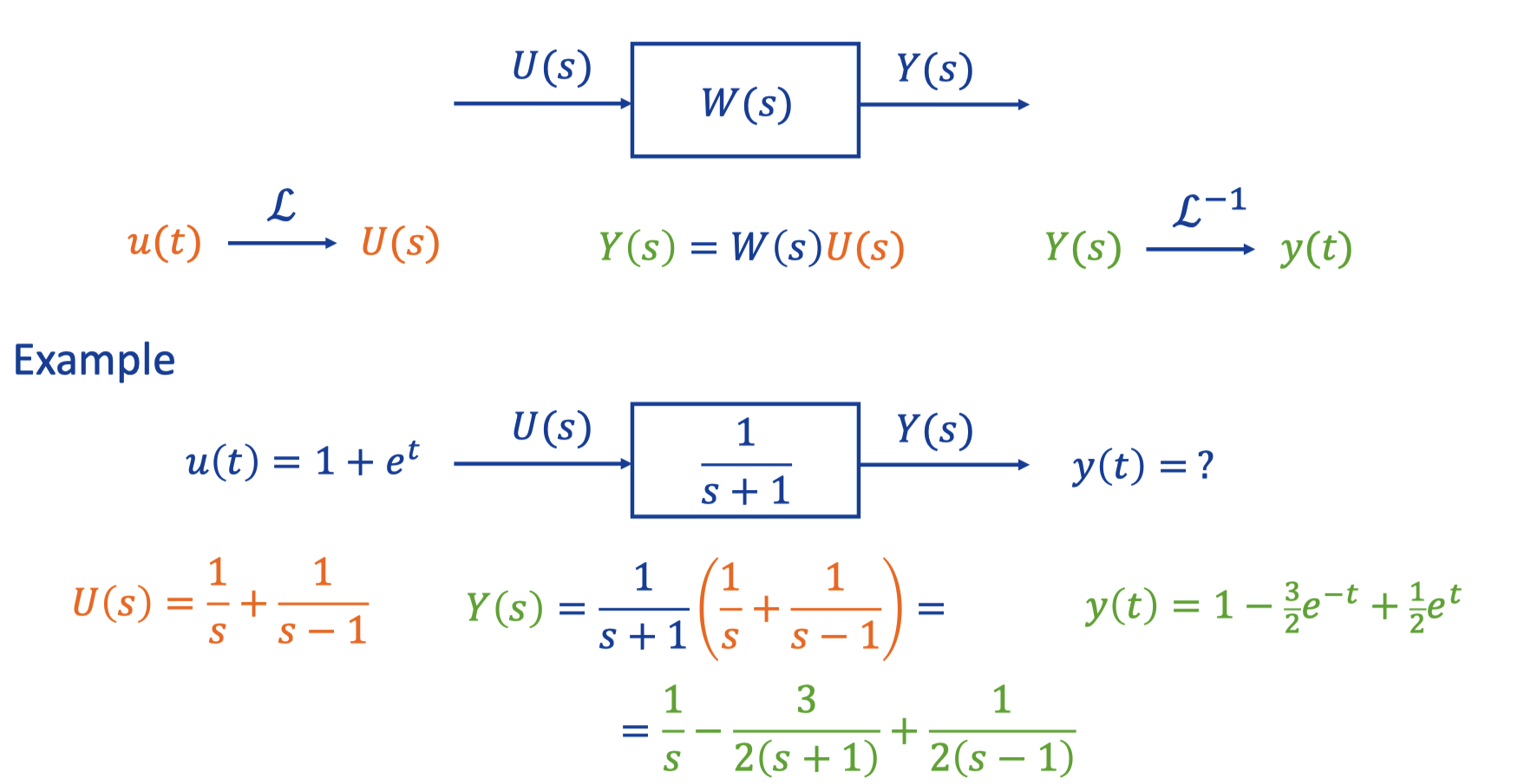
VIII. General forced response

IX. Steady-state value

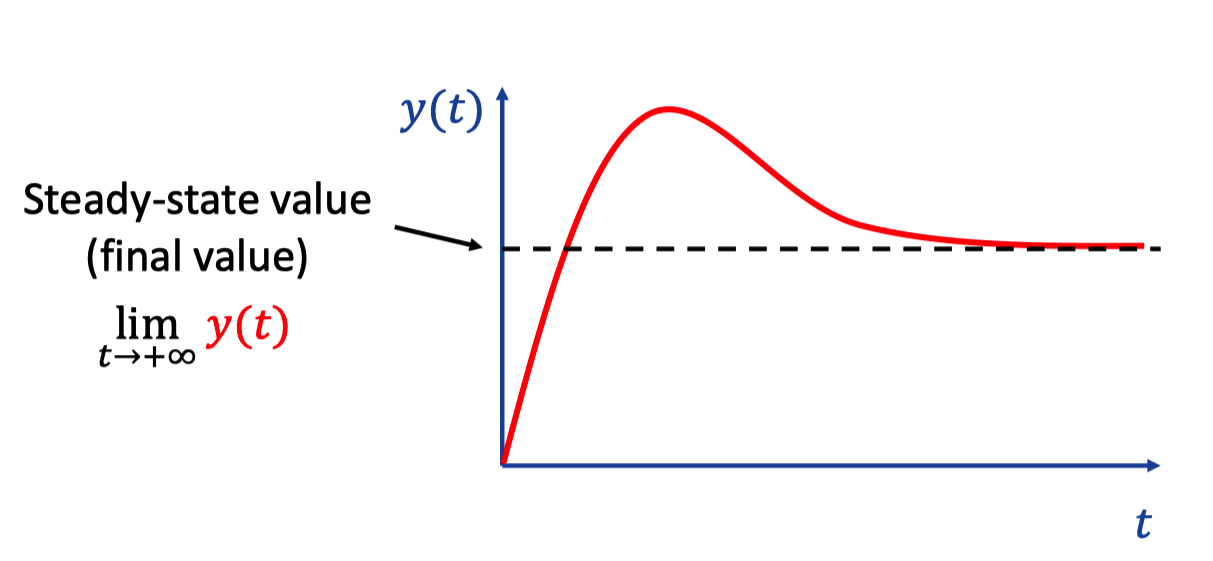
1. Final value thorem

If every pole of Y(s) is either in the negative half-plane (In complex plane), or at the origin and Y(s) has at most a single pole at the origin, then

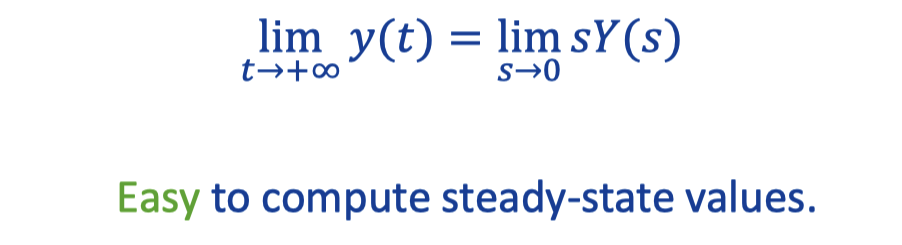
a. Example

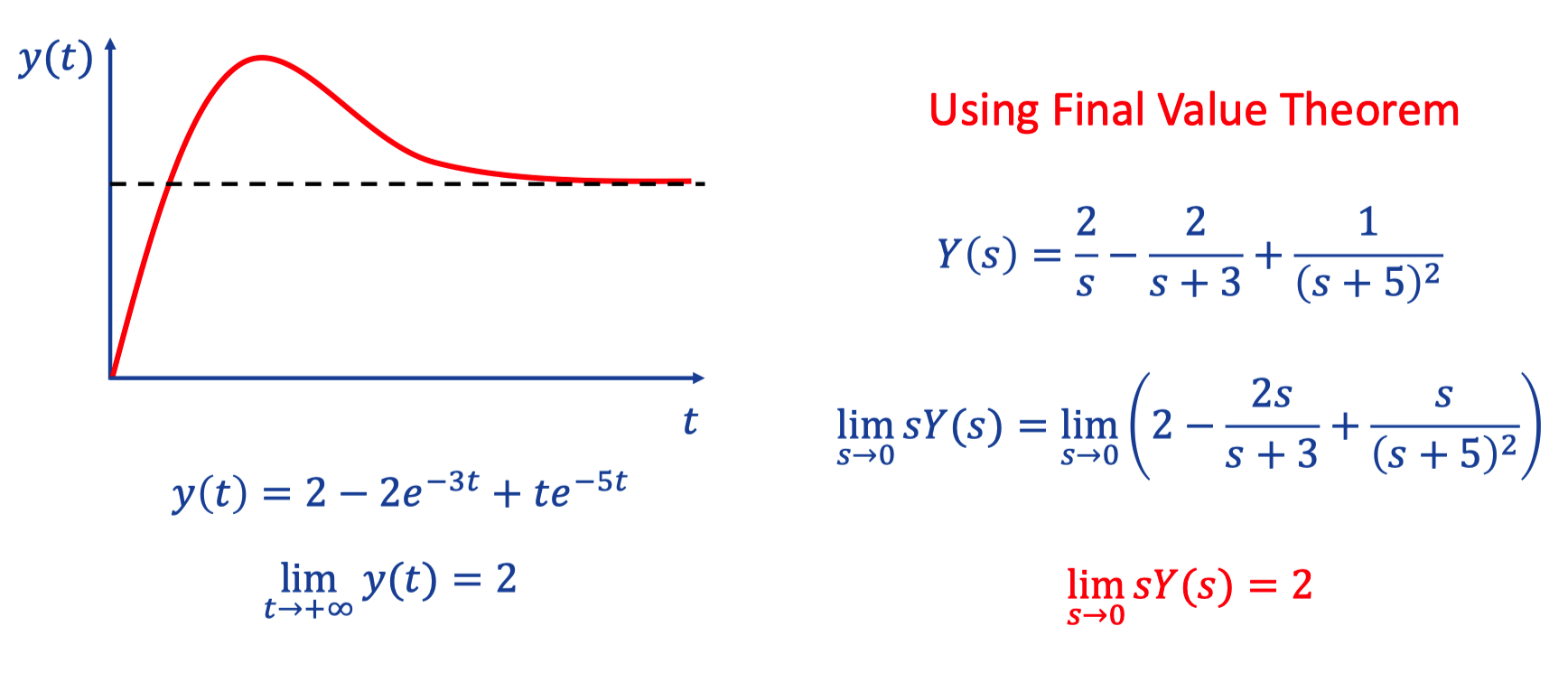
• **Note that the euqation should satisfies conditions**

b. Anti-example

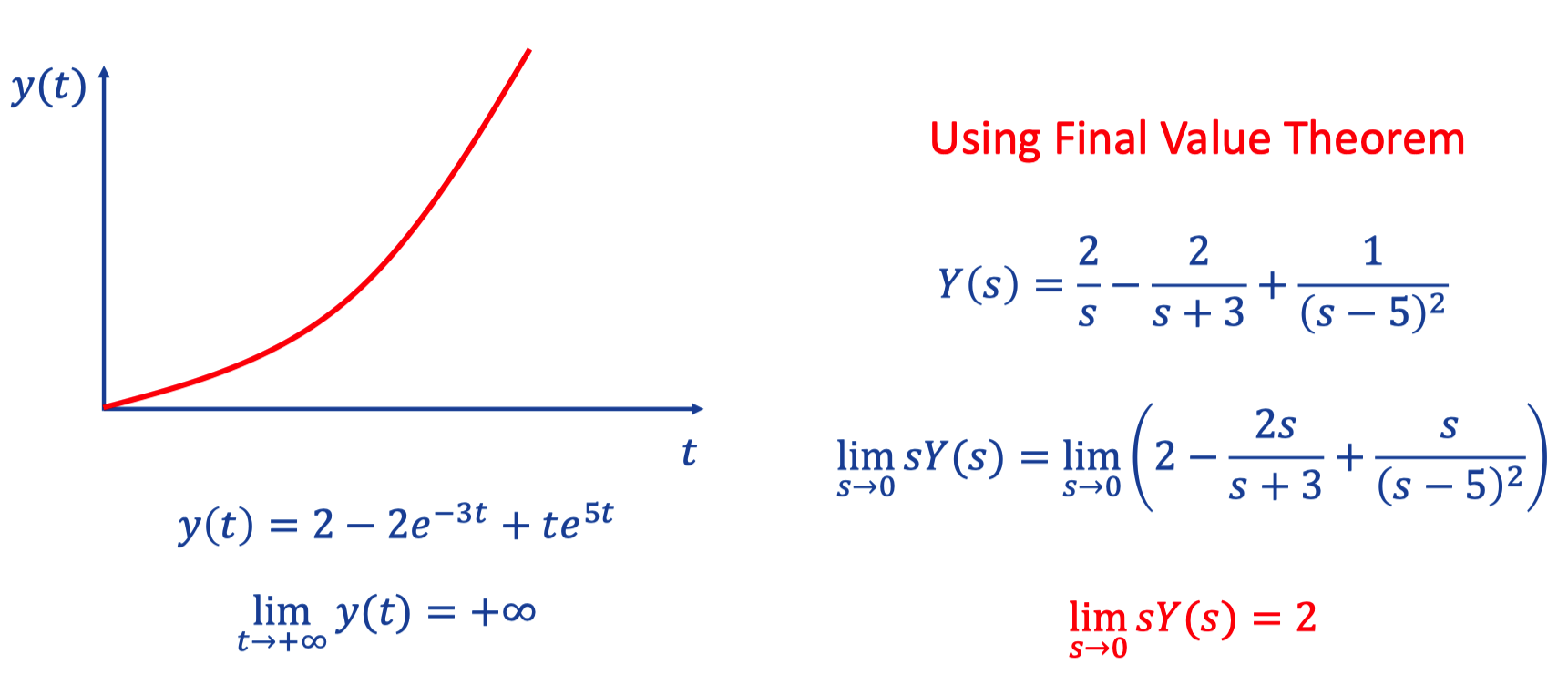
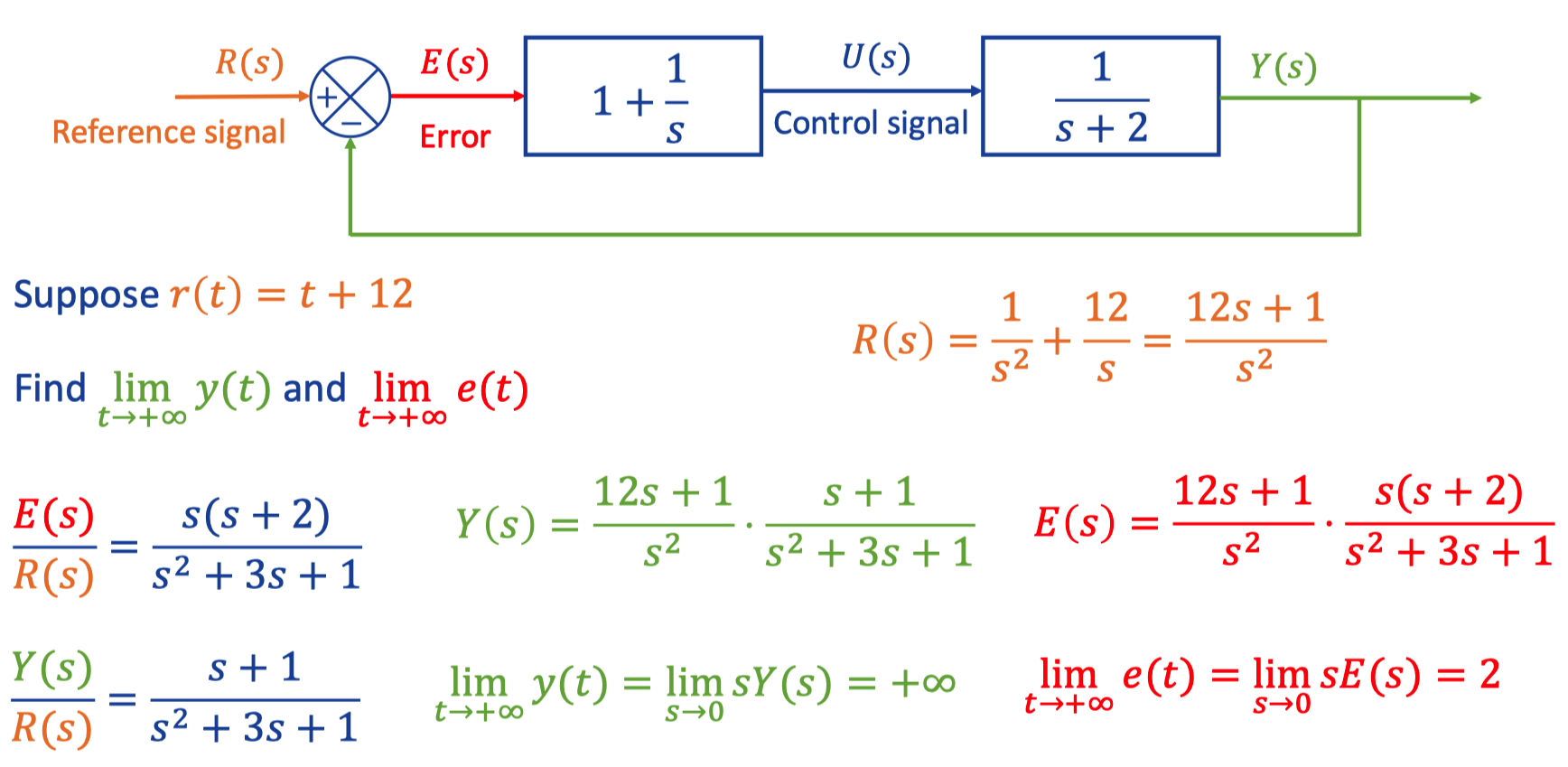
X. Closed-loop system

1. Two basic type

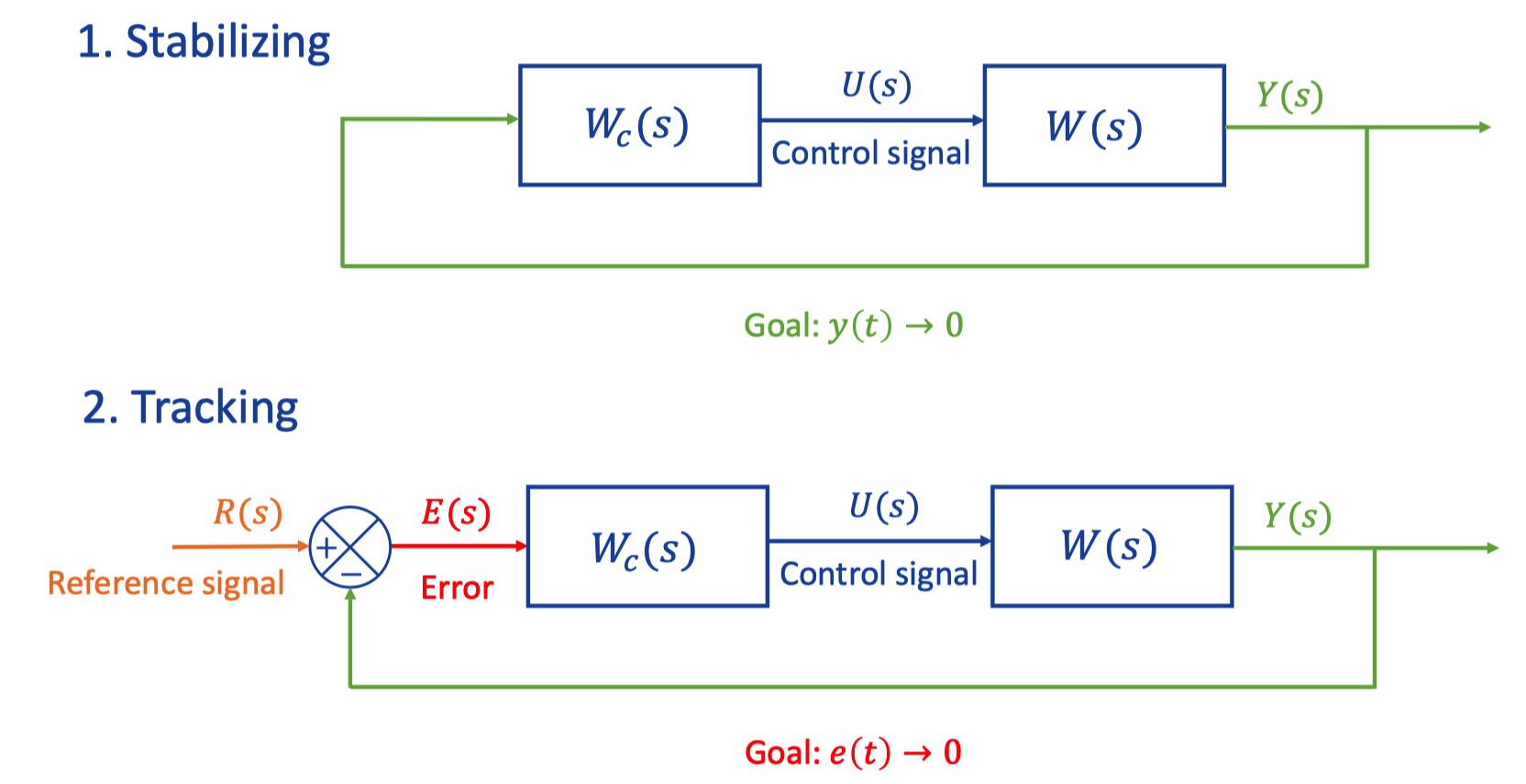
Controller -> System

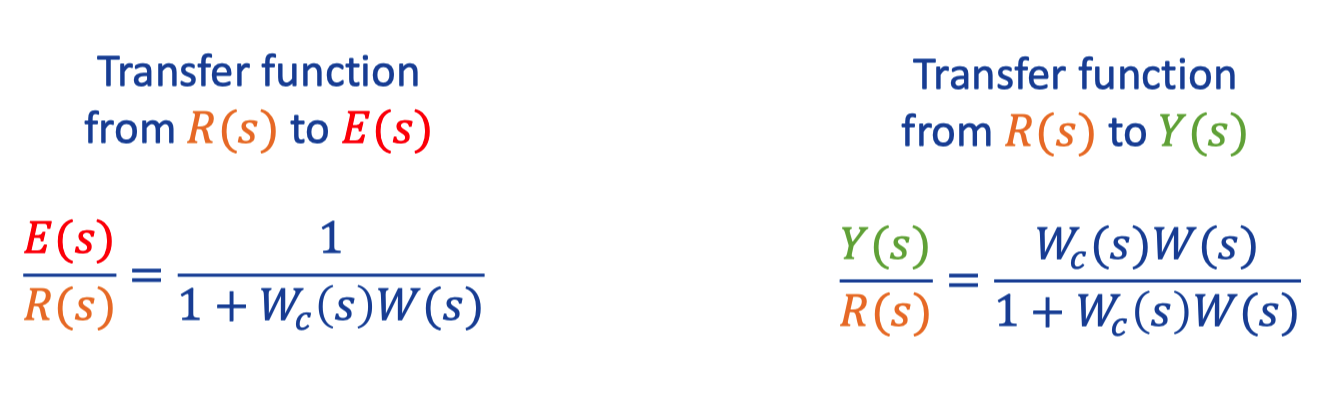
2. Example

a. eg1

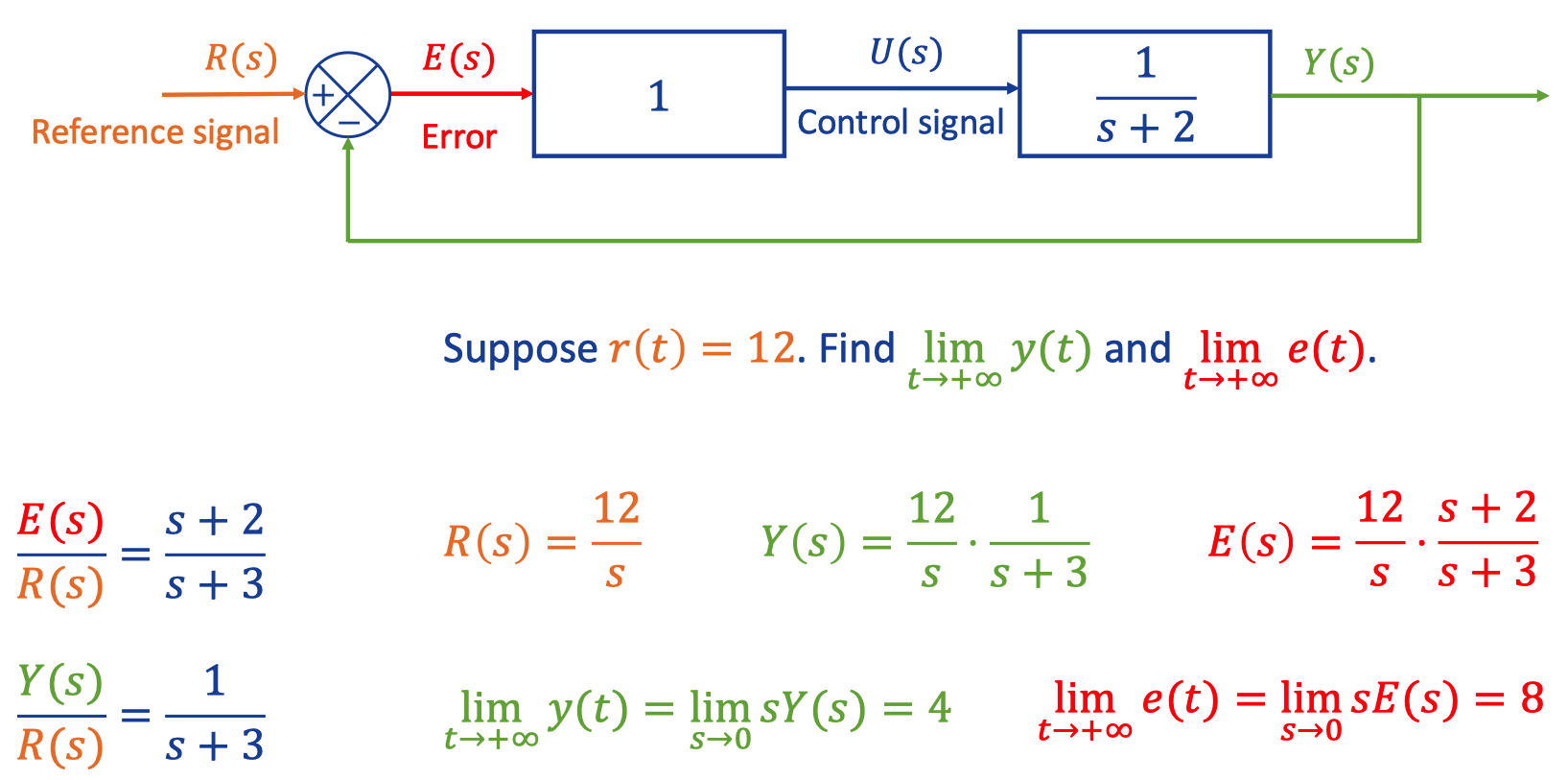
b. eg2