Let’s see then.

Table of Contents

1. Lec 5 State-space representation and transition of a linear system
   1. I. Classical vs. modern control theory
      1. a. Classical contorl theory
      2. b. Modern control theory
      3. c. SISO Control system
      4. d. E.G. Missile Launcher system
      5. e. MIMO Control system
      6. f. E.G. Boiler Generator
   2. II. State-space representation
      1. 1. Definition
      2. 2. Some classes of linear dynamical systems
      3. 3. Block diagram (eg)
      4. 4. E.g.
      5. 5. Note that the space rep is not unique.
         1. a. Case 1
         2. b. Case 2
      6. 6. Another way to derive the equation.
         1. a. E.g. RLC circuit
         2. b. E.g. Mass-spring-damper system
   3. III. State Vector
   4. IV*. Linear Algebra - pre skill tree.
   5. V. Transition between representations
      1. a. E.g.
      2. b. Controllable Canonical Form
      3. c. Observable Canonical Form
      4. d. Diagonal Canonical Form
      5. e. E.g
      6. f. Derive input & output representation
      7. g. E.g.
      8. h. Transfer matrix
      9. i. E.g.
      10. j. Addition

Lec 5 State-space representation and transition of a linear system

I. Classical vs. modern control theory

a. Classical contorl theory

• rapidly provides stability and transient information for deigns
• In MIMO control system, it would become cumbersome, which is not convenient to use.

b. Modern control theory

• Richer and more global representation, is enabling the represenation, in the form of a matrix of any system: invariant or non-invariant, linear or non- linear, SISO or MIMO, continuous or discrete.
• Time domain analysis, including state-space representation, which is internal representation.
• Additionaly to input and output characteristics. The more information of the system is feedback, the more complex system we can design.

c. SISO Control system

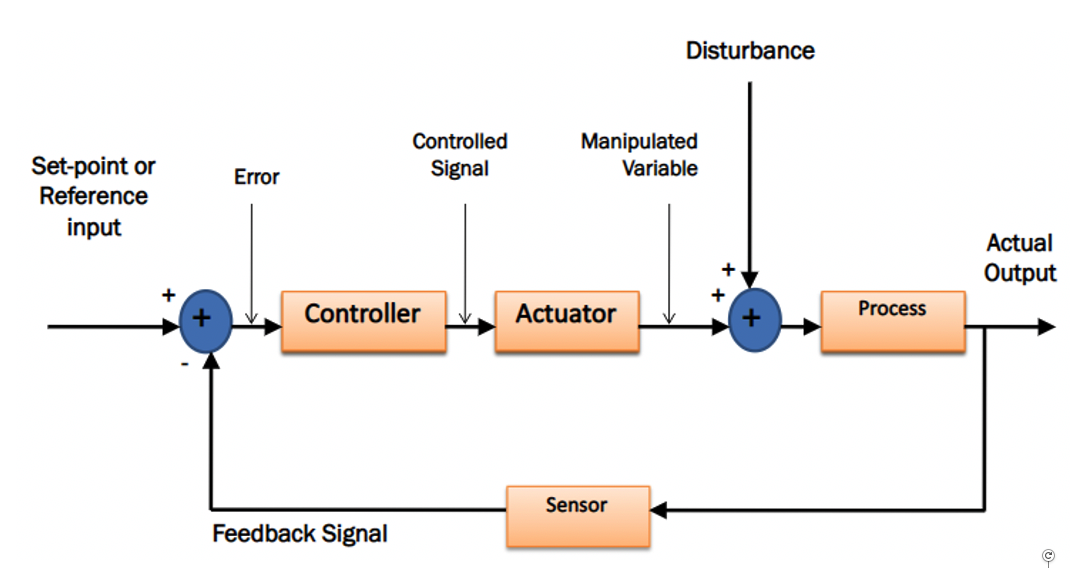
• physical process - a sustained phenomenon or one marked by gradual changes through a series of states;

d. E.G. Missile Launcher system

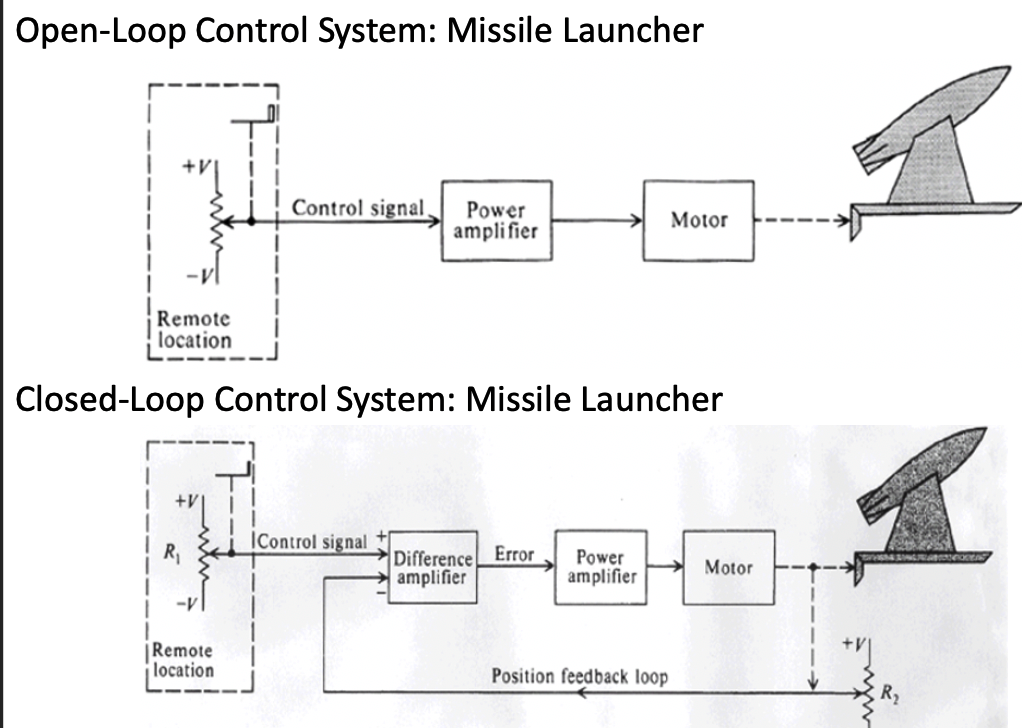
If we know the transfer function of Power Amplifier and Motor, we can make a good approach using classical method in both open and closed loop.

e. MIMO Control system

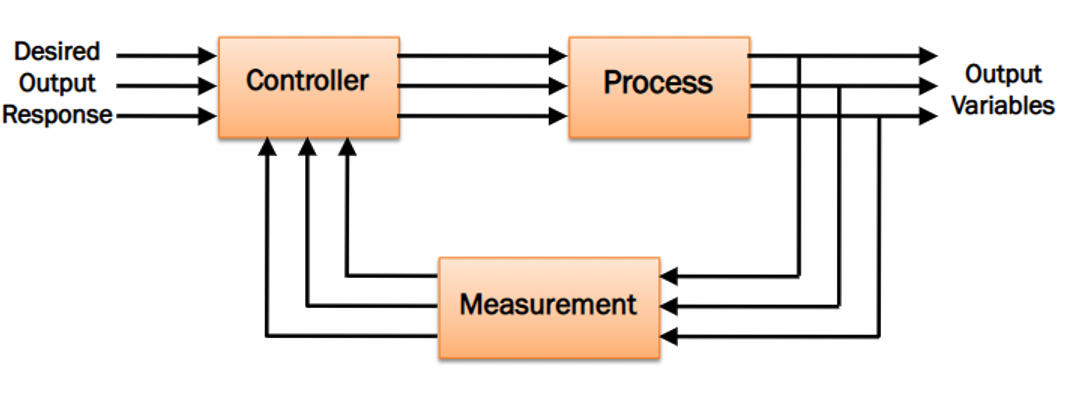
For such system, in order to apply classical approaches, we have to find sets of transfer functions for all pairs of inputs and outputs.

f. E.G. Boiler Generator

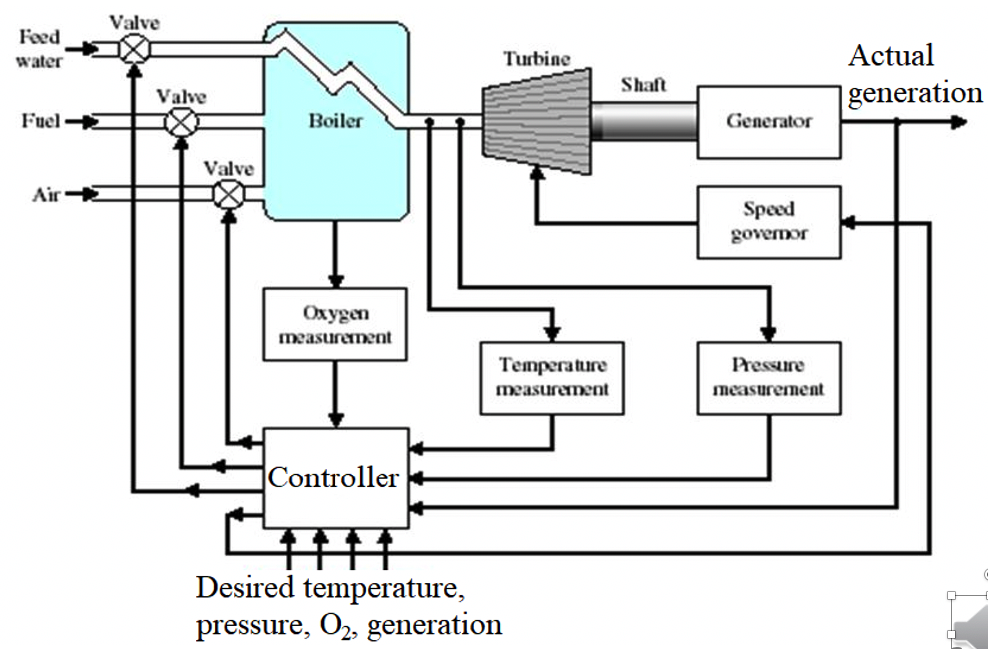
Here we have four outputs and four inputs. *Speed governor is also one of the inputs.

To use classical method, 16 transfer functions must be find, which make it cumbersome to analysis.

In some cases, we may neglect some parts of the system, we may lose important information and can’t guarantee the performance of control we want.

So using state-space representation makes it a lot easier.

II. State-space representation

1. Definition

Here, in addition to control u and output y, we use the state x of t in order to obtain so called internal representation.

The state is a vector quantity, defined it at any instant, which you present the set of information and energy stored by the system by the instant t.

2. Some classes of linear dynamical systems

3. Block diagram (eg)

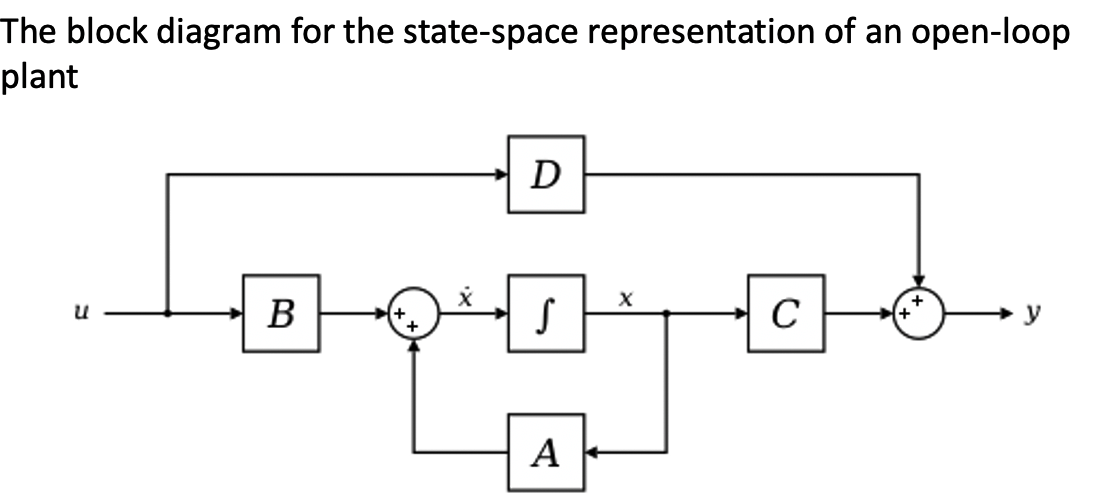
4. E.g.

5. Note that the space rep is not unique.

a. Case 1

It’s clear that it goes with your definition of x.

b. Case 2

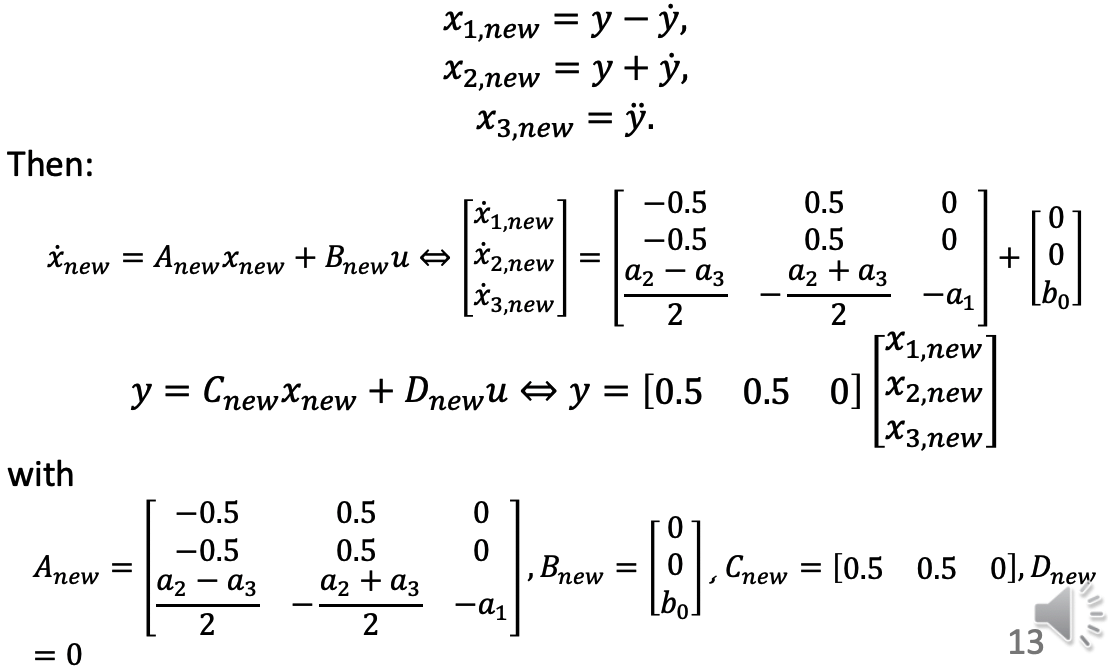
Yet, they represent the same system.

6. Another way to derive the equation.

Directly from the free body diagram.

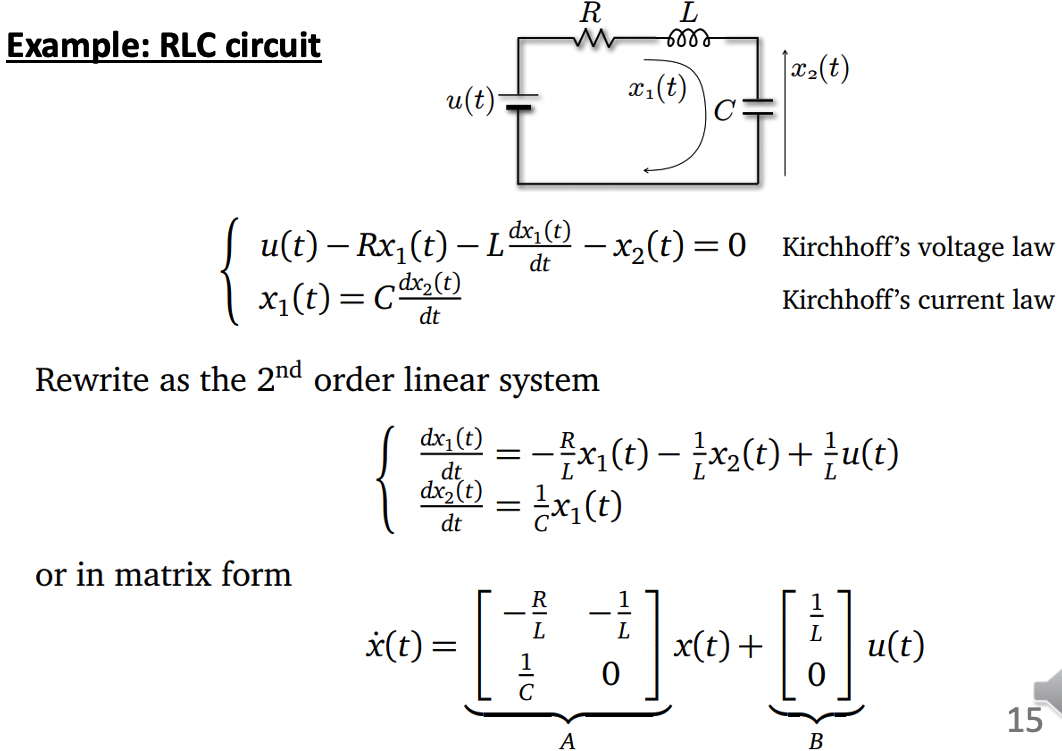
a. E.g. RLC circuit

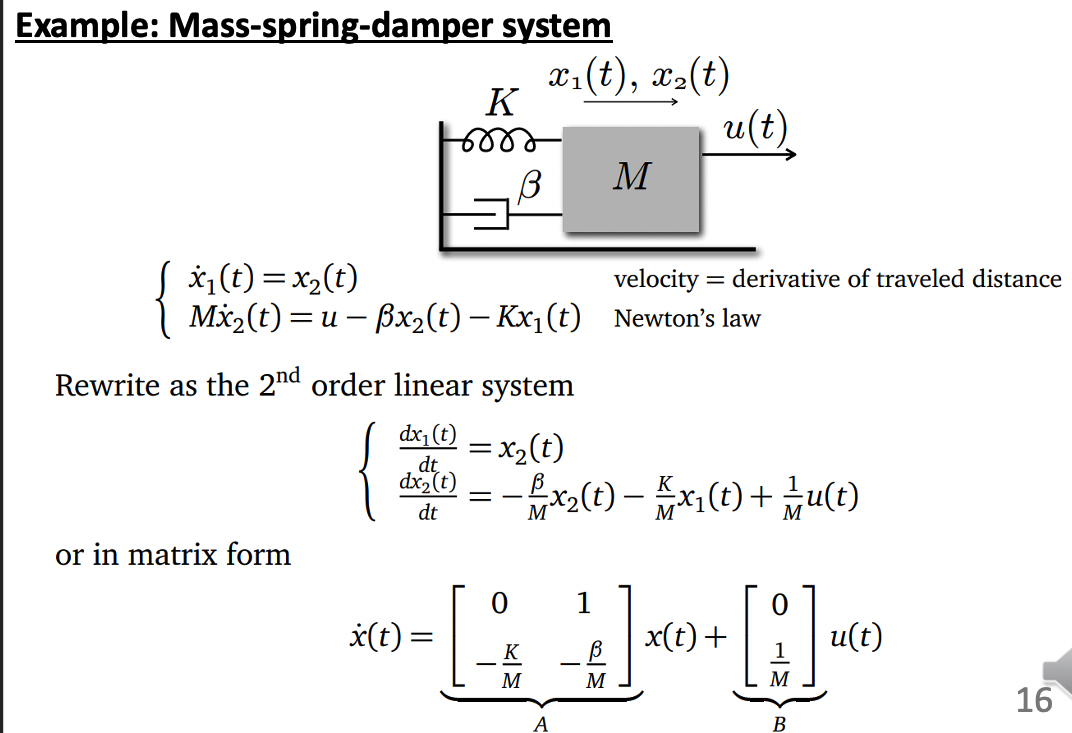
b. E.g. Mass-spring-damper system

III. State Vector

IV*. Linear Algebra - pre skill tree.

V. Transition between representations

a. E.g.

• Note that the term, derivative of u is not allowed in the state-space representation

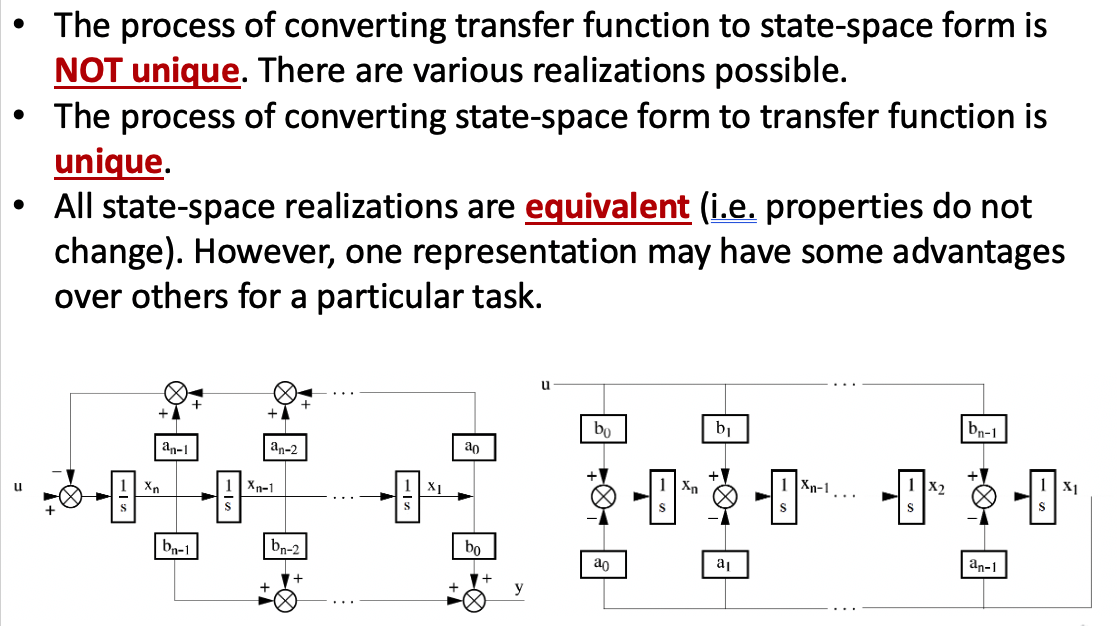
b. Controllable Canonical Form

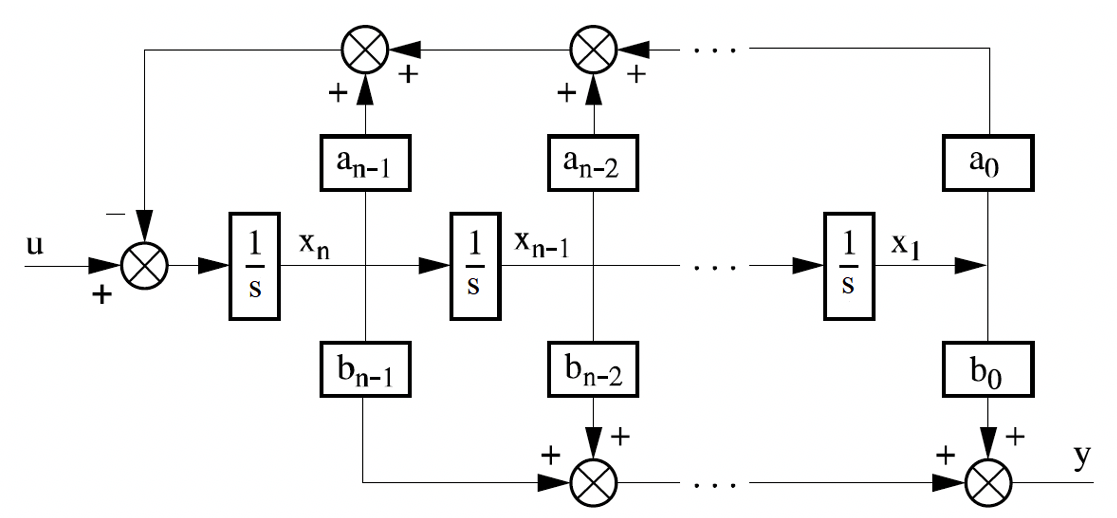
c. Observable Canonical Form

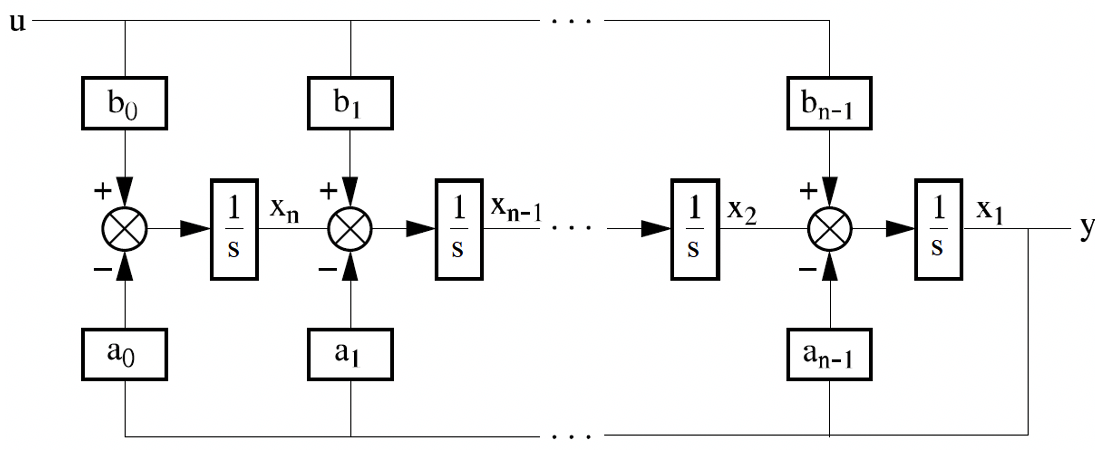
d. Diagonal Canonical Form

• Greatly simplify the calculatio

e. E.g

f. Derive input & output representation

Despite the fact that the state-space rep varies while the transfer function stays unique.

g. E.g.

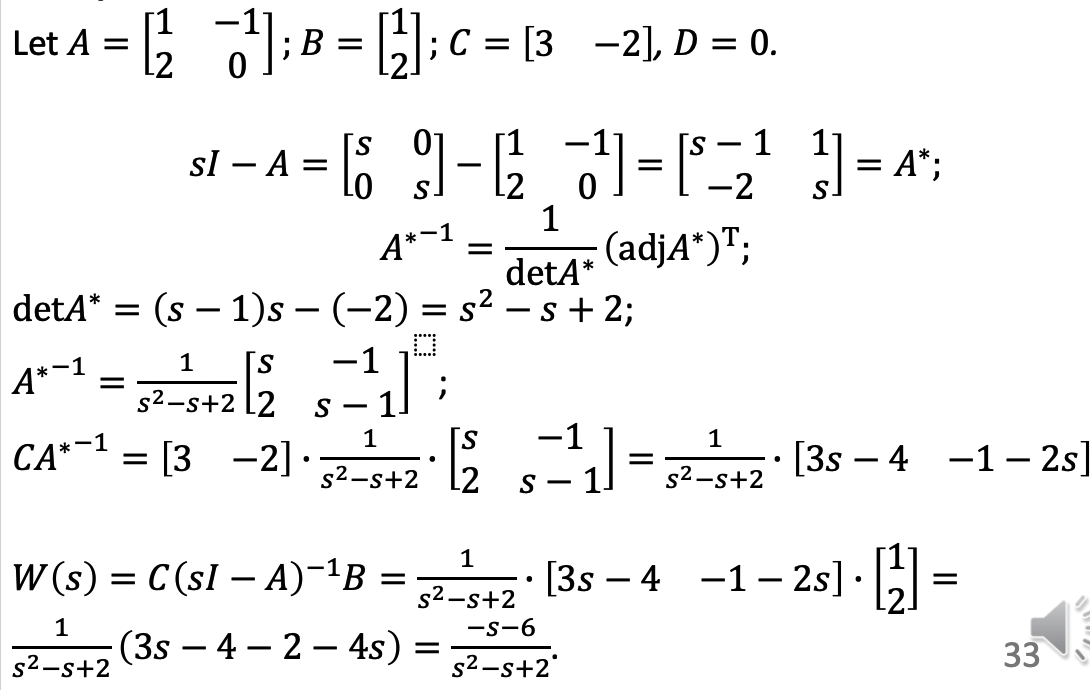
h. Transfer matrix

i. E.g.

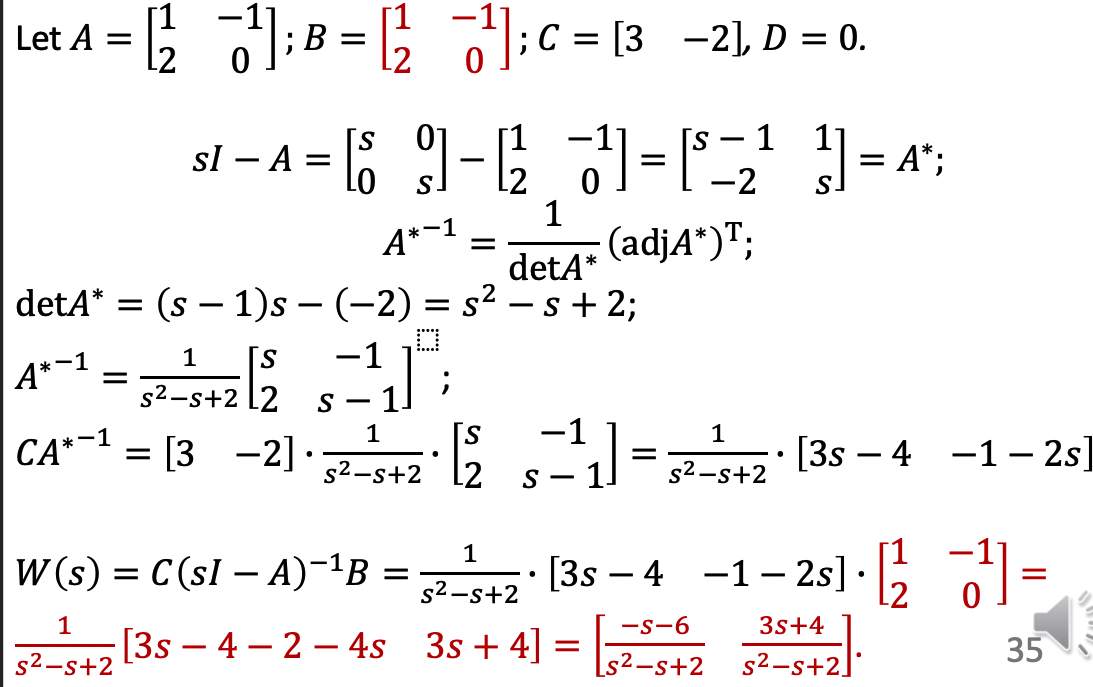
j. Addition