Younger than I thought.

Table of Contents

1. Lec 7 Controllability and Observability
   1. I. LA Recall
      1. a. Rank of matrix
   2. II. Controllability
      1. a. Definition
      2. b. Example.
      3. c . Definition 2
      4. d. Example
      5. e. Theorem
      6. d. Condition
   3. III. Output controbility
      1. a . Definition
      2. b. Theorem
   4. IV. Reachability
      1. a. Definition
   5. V. Stabilizability
      1. a. Definition
   6. VI. Observability
      1. a. Definition
      2. b. Theorem
      3. c. Condition
   7. VII. Detectability
      1. a. Definition

Lec 7 Controllability and Observability

I. LA Recall

a. Rank of matrix

The rank of a matrix 𝐴 is the dimension of the vector space generated (or spanned) by its columns. This corresponds to the maximal number of linearly independent columns of 𝐴.

In MATLAB, using rank() would be quick.

II. Controllability

a. Definition

A system is said to be completely state controllable if it is possible to transfer the system states from any initial state 𝑥(𝑡0) to any other desired state 𝑥(𝑡1) in a desired finite time interval 𝑡1 by unconstrained control vector 𝑢 𝑡 . Otherwise the system is not completely state controllable.

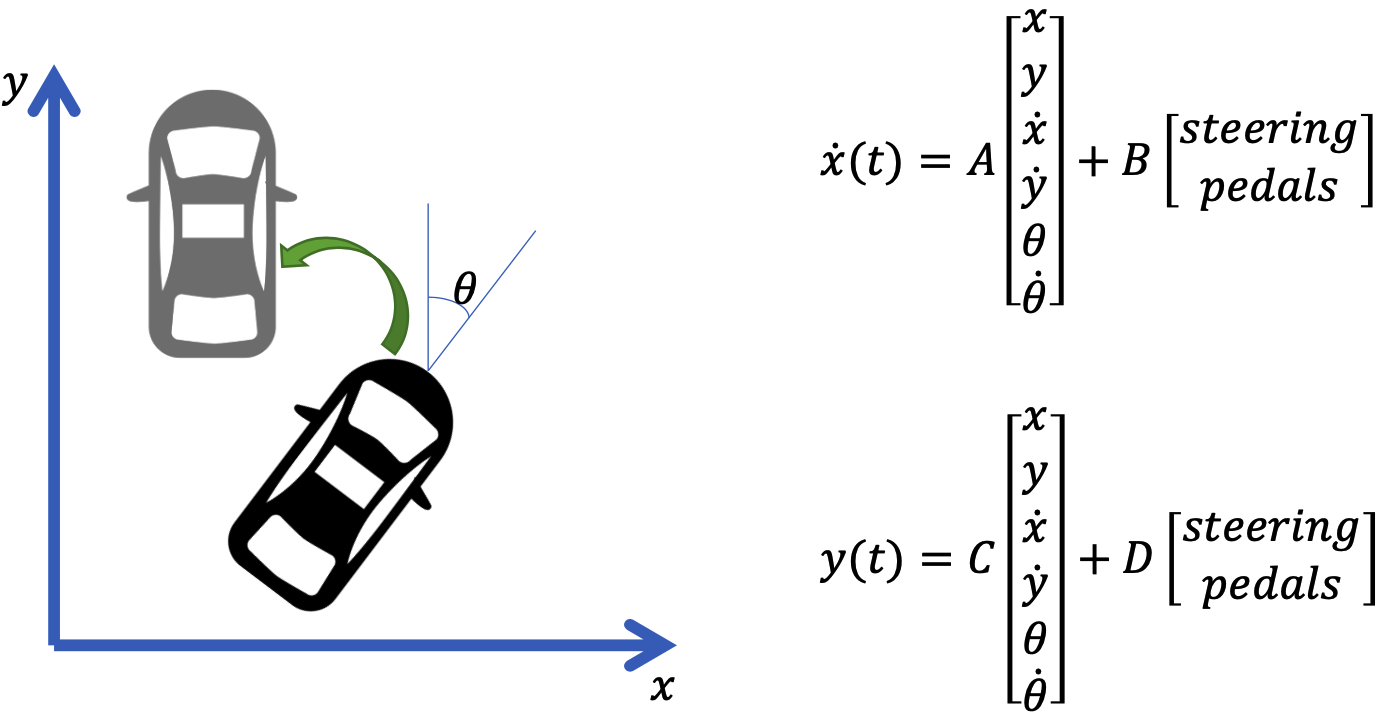
• if the system is controllable, the car can be moved to a desired position from any point in finite time.
• Unstrained control, it’s more theoretical.
• Note that not all parts are controllable and who’s in charge of the system - Matrix B.

b. Example.

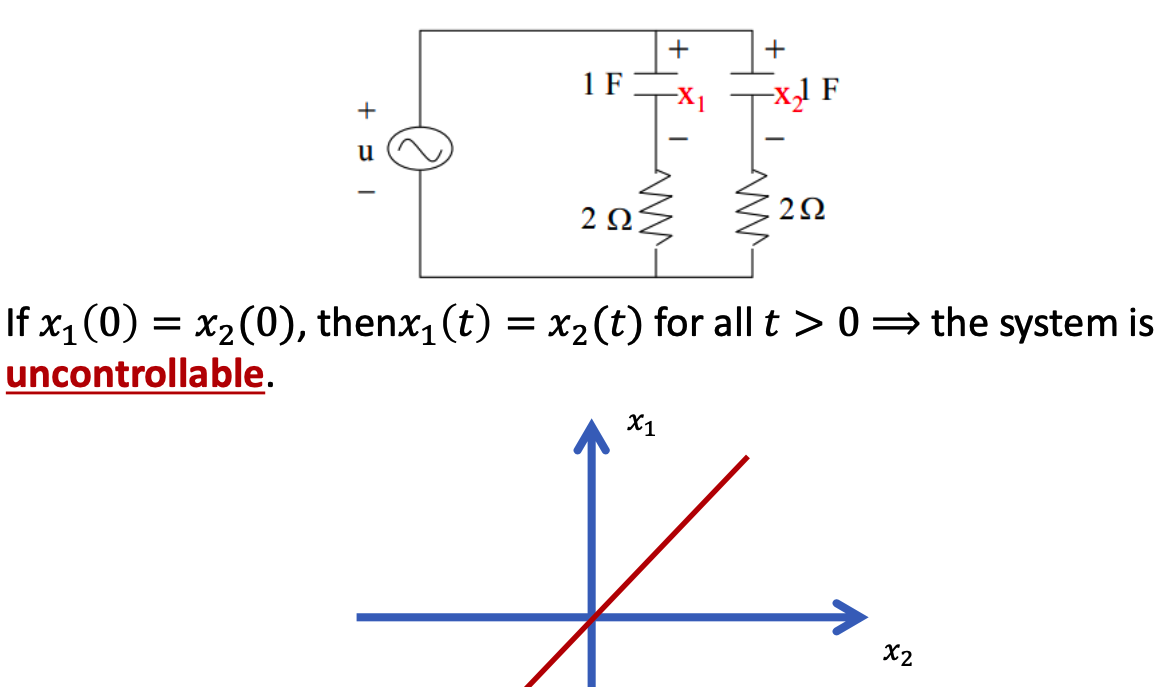
c . Definition 2

A way to calculate the coresponding u.

Here, Matrix W_c is usually called Controllability Gramian

• In linear algebra, the Gram matrix (or Gramian matrix, Gramian) of a set of vectors in an inner product space is the Hermitian matrix of inner products, whose entries are given by ${\displaystyle G_{ij}=\left\langle v_{i},v_{j}\right\rangle }$https://en.wikipedia.org/wiki/Gramian_matrix#cite_note-HJ-7.2.10-1)

  An important application is to compute linear independence: a set of vectors are linearly independent if and only if the Gram determinant (the determinant of the Gram matrix) is non-zero.

d. Example

e. Theorem

The following statements are equivalent:

S1) The pair 𝐴, 𝐵 is controllable;

S2) 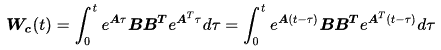is nonsigular for any t>0

S3) The controllability matrix 𝑄𝑐 ∈ 𝑅𝑛×𝑛𝑚:

​ 𝑄𝑐 =[𝐵,𝐴𝐵,.$𝐴^{𝑛−1}$𝐵]

S4)𝑟𝑎𝑛𝑘 (𝜆𝑖𝐼−𝐴⋮𝐵 )=𝑛 for all eigenvalues 𝜆𝑖 of 𝐴.

d. Condition

The controllability matrix 𝑄𝑐 ∈ 𝑅𝑛×𝑛𝑚 has rank n:

• The controllability matrix 𝑄𝑐 is square matrix if the system is single input only.
• If the matrix 𝑄𝑐 has rank less than 𝑛, this condition does not give which states are uncontrollable and the rest are controllable.
• If there is any 𝑛 × 𝑛 submatrix of 𝑄𝑐 with nonzero determinant, the matrix 𝑄𝑐 has rank 𝑛.
• The matrix 𝑄𝑐 has rank 𝑛 if the matrix 𝑀 = ${𝑄𝑐^𝑇 }$𝑄𝑐 (or 𝑀 = 𝑄𝑐${𝑄𝑐^𝑇 }$) has nonzero determinant.

In MATLAB, ctrb(A,B) returns the controllability matrix.

III. Output controbility

a . Definition

A system is said to be completely output controllable if it is possible to transfer the system output from any 𝑦($𝑡_0$) to any other desired output 𝑦($𝑡_1$) in a desired finite time interval $𝑡_1$ by unconstrained control vector 𝑢(𝑡).

In this case, we do not care controllability of each state, but the output.

b. Theorem

The necessary and sufficient condition for the system to be output controllable is that the rank of the output controllability matrix

​ 𝑄𝑐𝑜 = [𝐶𝐵,𝐶𝐴𝐵,.𝐶$𝐴^{𝑛−1}$𝐵,𝐷]

has rank 𝑝, where 𝑝 is a dimension of output vector 𝑦.

• A controllable system is not necessarily output controllable!
• An output controllable system is not necessarily state controllable!

IV. Reachability

a. Definition

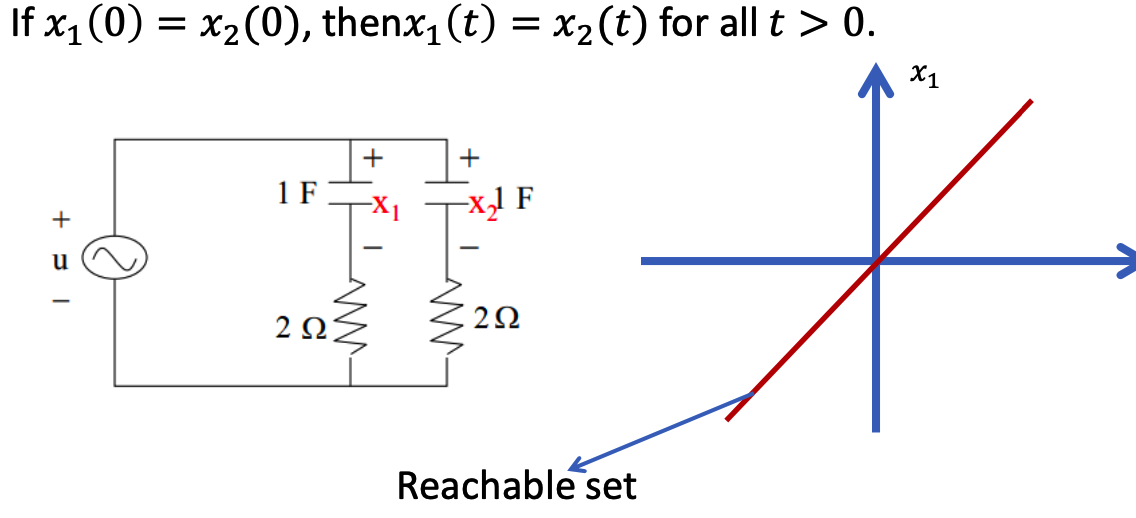
A particular state $𝑥_1$ is called reachable if there exists an input that transfers the state of the system from the initial state $𝑥_0$ to $x_1$ in some finite time interval $[t0, t).$

V. Stabilizability

a. Definition

A system is stabilizable if all states that cannot be reached decay to zero asymptotically.

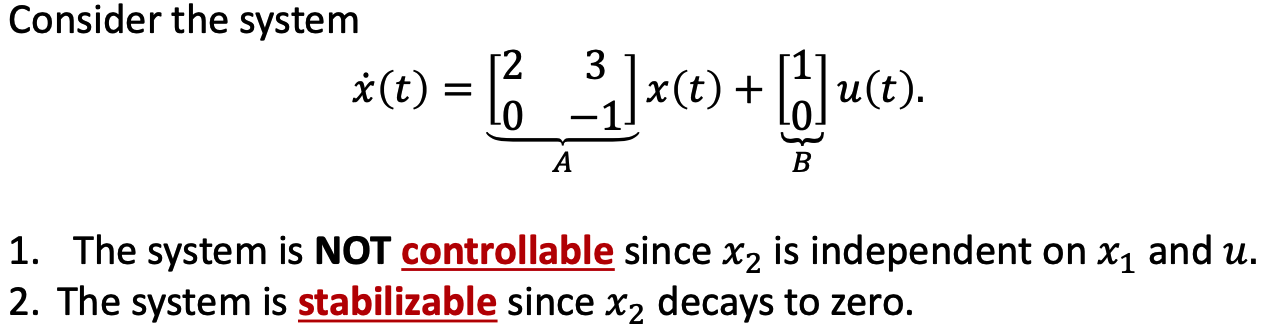
• In other words, in such system, limited states can be controlled to certain values in reachable set and others tend to zero.

VI. Observability

a. Definition

A system is said to be completely observable if every (critical) state 𝑥($𝑡_0$) can be completely identified by measurement of the output 𝑦(𝑡) over a finite time interval assuming that the control 𝑢(𝑡) is also available.

Controllability study the possibility to control the state from the input, while the observability study the possibility of estimating the state vector from the system output 𝑦(𝑡). If a system is not completely observable then some of its state variables are not practically measurable and are shielded from the observation.

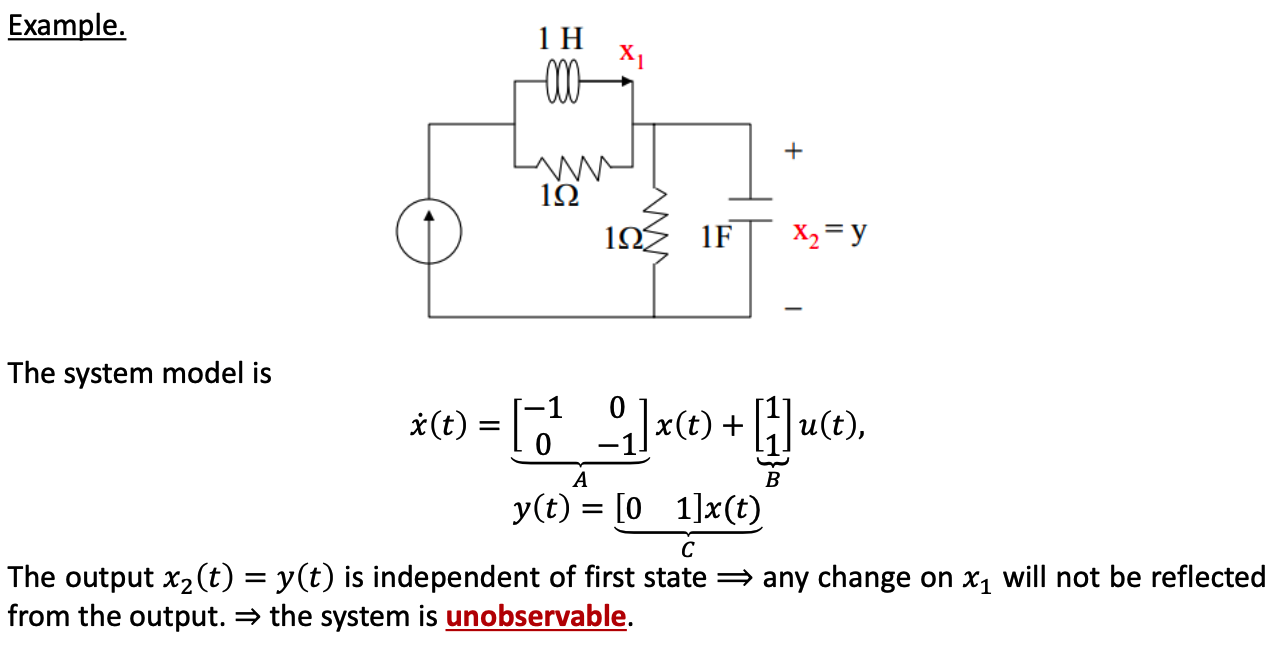
b. Theorem

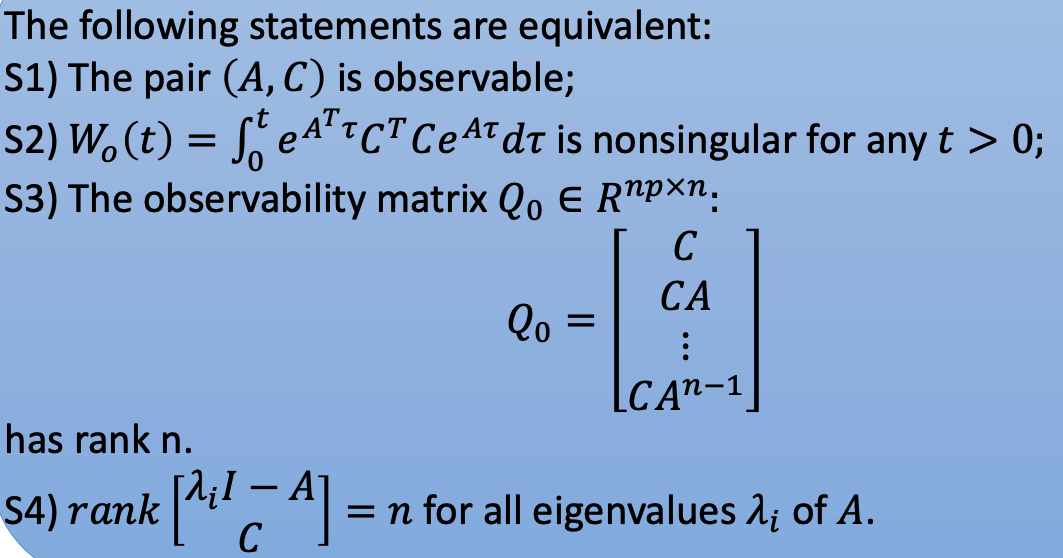
c. Condition

The Observability matrix $𝑄_𝑂$ ∈ $𝑅^{𝑛𝑃×𝑁}$ has rank n:

• The observability matrix $𝑄_𝑂$ is square matrix if the system is single output only.
• If the matrix 𝑄𝑜 has rank less than 𝑛, this condition does not give which states are unobservable and the rest are observable.
• Thematrix $𝑄_𝑂$ has rank 𝑛 if there is an 𝑛×𝑛 submatrix of 𝑄𝑜 that has nonzero determinant.
• The matrix 𝑄𝑜 has rank 𝑛 if the matrix 𝑀 = $𝑄_𝑂^𝑇 𝑄𝑜$ (or 𝑀 = $𝑄𝑜𝑄_𝑂^𝑇$ ) has nonzero determinant.

In MATLAB, you may use obsv(A,C)

VII. Detectability

a. Definition

A system is detectable if all states that cannot be observed decay to zero asymptotically.